【题目】计算:
(1)2x2﹣4x+1=0(配方法)
(2)﹣3x=1﹣x2
(3)2(x+2)2=x(x+2)
(4)(x+1)(x﹣1)+2(x+3)=8.
参考答案:
【答案】(1)x1=1+![]() ,x2=1﹣
,x2=1﹣![]() ;(2)x1=
;(2)x1=![]() ,x2=
,x2=![]() ;(3)x1=﹣4,x2=﹣2;
;(3)x1=﹣4,x2=﹣2;
(4)x1=1,x2=﹣3.
【解析】试题分析:(1)移项得出2x2-4x=-1,系数化成1得到x2-2x=-![]() ,配方得到(x-1)2=
,配方得到(x-1)2=![]() ,推出x-1=±
,推出x-1=±![]() ,求出即可;
,求出即可;
(2)移项得出x2-3x=1,配方得到(x-![]() )2=
)2=![]() ,推出x-
,推出x-![]() =±
=±![]() ,求出即可;
,求出即可;
(3)将方程移项后,方程的左边可以进行因式分解,应用因式分解法解答.
(4)先将方程展开,变为一般形式,再根据十字相乘法将方程的左边进行因式分解解答.
试题解析:(1)2x2﹣4x+1=0,
2x2﹣4x=﹣1,
x2﹣2x=﹣![]() ,
,
(x﹣1)2=![]() ,
,
x﹣1=±![]() ,
,
解得x1=1+![]() x2=1﹣
x2=1﹣![]()
(2)﹣3x=1﹣x2,
x2﹣3x=1,
(x﹣![]() )2=
)2=![]() ,
,
x﹣![]() =±
=±![]() ,
,
解得x1=![]() ,x2=
,x2=![]() ;
;
(3)2(x+2)2=x(x+2),
2(x+2)2﹣x(x+2)=0,
(2x+4﹣x)(x+2)=0,
(x+4)(x+2)=0,
解得x1=﹣4,x2=﹣2;
(4)(x+1)(x﹣1)+2(x+3)=8,
x2﹣1+2x+6﹣8=0,
x2+2x﹣3=0,
(x﹣1)(x+3)=0,
解得x1=1,x2=﹣3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在菱形ABCD中,AC=2,BD=2
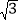 ,AC,BD相交于点O.
,AC,BD相交于点O.
(1)求边AB的长;
(2)如图2,将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处,绕点A左右旋转,其中三角板60°角的两边分别与边BC,CD相交于点E,F,连接EF与AC相交于点G.
①判断△AEF是哪一种特殊三角形,并说明理由;
②旋转过程中,当点E为边BC的四等分点时(BE>CE),求CG的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九2x=﹣6章算术》中记载:“今有人共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?”
译文:“假设有几个人共同出钱买鸡,如果每人出九钱,那么多了十一钱;如果每人出六钱,那么少了十六钱.问:有几个人共同出钱买鸡?鸡的价钱是多少?”设有x个人共同买鸡,根据题意列一元一次方程,正确的是( )

A. 9x+11=6x﹣16B. 9x﹣11=6x+16
C.
 D.
D. 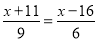
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A、B两点,与y轴交于C点,直线BD交抛物线于点D,并且D(2,3),tan∠DBA=
 .
.(1)求抛物线的解析式;
(2)已知点M为抛物线上一动点,且在第三象限,顺次连接点B、M、C、A,求四边形BMCA面积的最大值;
(3)在(2)中四边形BMCA面积最大的条件下,过点M作直线平行于y轴,在这条直线上是否存在一个以Q点为圆心,OQ为半径且与直线AC相切的圆?若存在,求出圆心Q的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线过点A(2,0),B(﹣1,0),与y轴交于点C,且OC=2,求这条抛物线的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了备战学校体育节的乒乓球比赛活动,某班计划买5副乒乓球拍和若干盒乒乓球(多于5盒).该班体育委员发现在学校附近有甲、乙两家商店都在出售相同品牌的乒乓球拍和乒乓球,乒乓球拍每副售价100元,乒乓球每盒售价25元.经过体育委员的洽谈,甲商店给出每买一副乒乓球拍送一盒乒乓球的优惠;乙商店给出乒乓球拍和乒乓球全部九折的优惠.
(1)若这个班计划购买6盒乒乓球,则在甲商店付款 元,在乙商店付款 元;
(2)当这个班购买多少盒乒乓球时,在甲、乙两家商店付款相同?
-
科目: 来源: 题型:
查看答案和解析>>【题目】类比探究:
(1)如图1,等边△ABC内有一点P,若AP=8,BP=15,CP=17,求∠APB的大小;(提示:将△ABP绕顶点A旋转到△ACP′处)
(2)如图2,在△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点,且∠EAF=45°.求证:EF2=BE2+FC2;
(3)如图3,在△ABC中,∠C=90°,∠ABC=30°,点O为△ABC内一点,连接AO、BO、CO,且∠AOC=∠COB=∠BOA=120°,若AC=1,求OA+OB+OC的值.

相关试题

