【题目】如图,已知抛物线y=ax2+bx﹣2(a≠0)与x轴交于A、B两点,与y轴交于C点,直线BD交抛物线于点D,并且D(2,3),tan∠DBA=![]() .
.
(1)求抛物线的解析式;
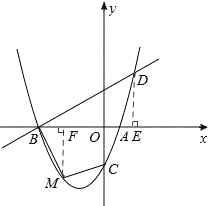
(2)已知点M为抛物线上一动点,且在第三象限,顺次连接点B、M、C、A,求四边形BMCA面积的最大值;
(3)在(2)中四边形BMCA面积最大的条件下,过点M作直线平行于y轴,在这条直线上是否存在一个以Q点为圆心,OQ为半径且与直线AC相切的圆?若存在,求出圆心Q的坐标;若不存在,请说明理由.

参考答案:
【答案】解:(1)如答图1,过点D作DE⊥x轴于点E,则DE=3,OE=2。
∵![]() ,∴BE=6。
,∴BE=6。
∴OB=BE﹣OE=4。∴B(﹣4,0)。
∵点B(﹣4,0)、D(2,3)在抛物线y=ax2+bx﹣2(a≠0)上,
∴![]() ,解得
,解得![]() 。
。
∴抛物线的解析式为: ![]() 。
。
(2)在抛物线![]() 中,
中,
令x=0,得y=﹣2,∴C(0,﹣2)。
令y=0,得x=﹣4或1,∴A(1,0)。
设点M坐标为(m,n)(m<0,n<0)。
如答图1,过点M作MF⊥x轴于点F,则MF=﹣n,OF=﹣m,BF=4+m。
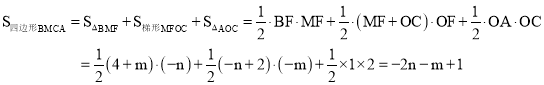
∵点M(m,n)在抛物线![]() 上,∴
上,∴![]() ,代入上式得:
,代入上式得:
![]() ,
,
∴当m=﹣2时,四边形BMCA面积有最大值,最大值为9。
(3)假设存在这样的⊙Q,
如答图2所示,设直线x=﹣2与x轴交于点G,与直线AC交于点F
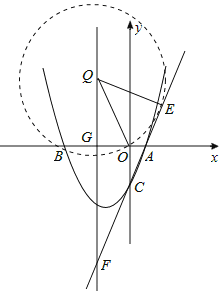
设直线AC的解析式为y=kx+b,
将A(1,0)、C(0,﹣2)代入得:
![]() ,解得:
,解得: ![]() 。
。
∴直线AC解析式为:y=2x﹣2。
令x=﹣2,得y=﹣6,∴F(﹣2,﹣6),GF=6。
在Rt△AGF中,由勾股定理得:
![]() 。
。
设Q(﹣2,q),则在Rt△AGF中,由勾股定理得:
![]() 。
。
设⊙Q与直线AC相切于点E,则QE=OQ=![]() 。
。
在Rt△AGF与Rt△QEF中,
∵∠AGF=∠QEF=90°,∠AFG=∠QFE,∴Rt△AGF∽Rt△QEF。
∴![]() ,即
,即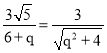 。
。
化简得: ![]() ,解得q=4或q=﹣1。
,解得q=4或q=﹣1。
∴存在一个以Q点为圆心,OQ为半径且与直线AC相切的圆,点Q的坐标为(﹣2,4)或(﹣2,﹣1)。
【解析】(1)如答图1所示,利用已知条件求出点B的坐标,然后用待定系数法求出抛物线的解析式。
(2)如答图1所示,首先求出四边形BMCA面积的表达式,然后利用二次函数的性质求出其最大值。
(3)如答图2所示,首先求出直线AC与直线x=2的交点F的坐标,从而确定了Rt△AGF的各个边长;然后证明Rt△AGF∽Rt△QEF,利用相似线段比例关系列出方程,求出点Q的坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】由于受猪流感的影响,4月初某地猪肉价格大幅度下调,下调后每斤猪肉价格是原价格的
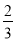 ,原来用60元买到的猪肉下调后可多买2斤.4月中旬,经专家研究证实,猪流感不是由猪传染,很快更名为甲型H1N1流感.因此,猪肉价格4月底开始回升,经过两个月后,猪肉价格上调为每斤14.4元.
,原来用60元买到的猪肉下调后可多买2斤.4月中旬,经专家研究证实,猪流感不是由猪传染,很快更名为甲型H1N1流感.因此,猪肉价格4月底开始回升,经过两个月后,猪肉价格上调为每斤14.4元.(1)求4月初猪肉价格下调后每斤多少元?
(2)求5、6月份猪肉价格的月平均增长率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是菱形,AC=8,BD=6,DH⊥AB于H.
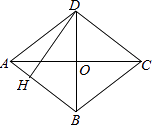
求:
(1)菱形ABCD的周长;
(2)求DH的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】先化简再求值:
(1)3(x2-2x-1)-4(3x-2)+2(x-1),其中x=﹣3;
(2)2a2﹣[
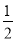 (ab﹣4a2)+8ab]﹣
(ab﹣4a2)+8ab]﹣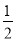 ab,其中a=1,b=
ab,其中a=1,b=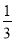 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】列一元一次方程解应用题:
某管道由甲、乙两工程队单独施工分别需要30天、20天.
(1)如果两队从管道两端同时施工,需要多少天完工?
(2)又知甲队单独施工每天需付200元施工费,乙队单独施工每天需付280元施工费,那么是由甲队单独施工,还是由乙队单独施工,还是由两队同时施工?请你按照少花钱多办事的原则,设计一个方案,并通过计算说明理由.
-
科目: 来源: 题型:
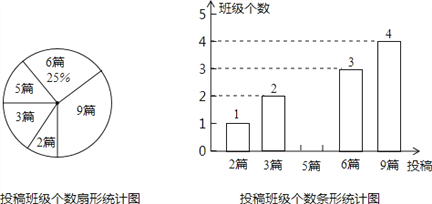
查看答案和解析>>【题目】为积极响应市政府提出的“建设美丽南宁”的号召,我市某校在八,九年级开展征文活动,校学生会对这两个年级各班内的投稿情况进行统计,并制成了如图所示的两幅不完整的统计图.
(1)求扇形统计图中投稿篇数为2所对应的扇形的圆心角的度数:
(2)求该校八,九年级各班在这一周内投稿的平均篇数,并将该条形统计图补充完整.
(3)在投稿篇数为9篇的四个班级中,八,九年级各有两个班,校学生会准备从这四个班中选出两个班参加全市的表彰会,请你用列表法或画树状图的方法求出所选两个班正好不在同一年级的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.a2·a3=a6
B.(a2)3=a5
C.(-2a2b)3=-8a6b3
D.(2a+1)2=4a2+2a+1
相关试题

