【题目】类比探究:
(1)如图1,等边△ABC内有一点P,若AP=8,BP=15,CP=17,求∠APB的大小;(提示:将△ABP绕顶点A旋转到△ACP′处)
(2)如图2,在△ABC中,∠CAB=90°,AB=AC,E、F为BC上的点,且∠EAF=45°.求证:EF2=BE2+FC2;
(3)如图3,在△ABC中,∠C=90°,∠ABC=30°,点O为△ABC内一点,连接AO、BO、CO,且∠AOC=∠COB=∠BOA=120°,若AC=1,求OA+OB+OC的值.

参考答案:
【答案】(1)150°;(2)见解析;(3)![]() .
.
【解析】
(1)根据△APB绕着点A逆时针旋转60°得到△ACP′,根据旋转变换前后的两个三角形全等,全等三角形对应边相等,全等三角形对应角相等以及等边三角形的判定和勾股定理逆定理即可得到结论;
(2)把△ABE绕点A逆时针旋转90°得到△ACE′,根据旋转的性质可得AE′=AE,CE′=CE,∠CAE′=∠BAE,∠ACE′=∠B,∠EAE′=90°,再求出∠E′AF=45°,从而得到∠EAF=∠E′AF,然后利用“边角边”证明△EAF和△E′AF全等,根据全等三角形对应边相等可得E′F=EF,再利用勾股定理列式即可得证;
(3)将△AOB绕点B顺时针旋转60°至△A′O′B处,连接OO′,根据直角三角形30°角所对的直角边等于斜边的一半求出AB=2AC,即A′B的长,再根据旋转的性质求出△BOO′是等边三角形,根据等边三角形的三条边都相等可得BO=OO′,等边三角形三个角都是60°求出∠BOO′=∠BO′O=60°,然后求出C、O、A′、O′四点共线,再利用勾股定理列式求出A′C,从而得到OA+OB+OC=A′C.
解:(1)如图1,将△APB绕着点A逆时针旋转60°得到△ACP′,
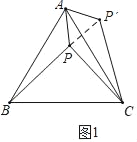
∴△ACP′≌△ABP,
∴AP′=AP=8、CP′=BP=15、∠AP′C=∠APB,
由题意知旋转角∠PA P′=60°,
∴△AP P′为等边三角形,
∴P P′=AP=8,∠A P′P=60°,
∵PP′2+P′C2=82+152=172=PC2,
∴∠PP′C=90°,
∴∠APB=∠AP′C=∠A P′P+∠P P′C=60°+90°=150°
(2)如图2,把△ABE绕着点A逆时针旋转90°得到△ACE′,
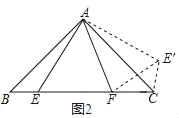
则AE′=AE,CE′=CE,∠CAE′=∠BAE,
∵∠BAC=90°,∠EAF=45°,
∴∠BAE+∠CAF=∠CAF+∠CAE′=∠FAE′=45°,
∴∠EAF=∠E′AF,且AE=AE',AF=AF,
∴△AEF≌△AE′F(SAS),
∴EF=E′F,
∵∠B+∠ACB=90°,
∴∠ACB+∠ACE′=90°,
∴∠FCE′=90°,
∴E′F2=CF2+CE′2,
∴EF2=BE2+CF2;
(3)如图3,将△AOB绕点B顺时针旋转60°至△A′O′B处,连接OO′,
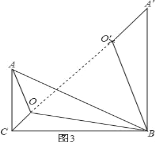
∵在Rt△ABC中,∠C=90°,AC=1,∠ABC=30°,
∴AB=2,
∴![]()
∵△AOB绕点B顺时针方向旋转60°,
∴△A′O′B如图所示;
∠A′BC=∠ABC+60°=30°+60°=90°,
∵∠ACB=90°,AC=1,∠ABC=30°,
∴AB=2AC=2,
∵△AOB绕点B顺时针方向旋转60°,得到△A′O′B,
∴A′B=AB=2,BO=BO′,A′O′=AO,
∴△BOO′是等边三角形,
∴BO=OO′,∠BOO′=∠BO′O=60°,
∵∠AOC=∠COB=∠BOA=120°,
∴∠COB+∠BOO′=∠BO′A′+∠BO′O=120°+60°=180°,
∴C、O、A′、O′四点共线,
在Rt△A′BC中,![]() ,
,
∴OA+OB+OC=A′O′+OO′+OC=A′C=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)2x2﹣4x+1=0(配方法)
(2)﹣3x=1﹣x2
(3)2(x+2)2=x(x+2)
(4)(x+1)(x﹣1)+2(x+3)=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线过点A(2,0),B(﹣1,0),与y轴交于点C,且OC=2,求这条抛物线的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了备战学校体育节的乒乓球比赛活动,某班计划买5副乒乓球拍和若干盒乒乓球(多于5盒).该班体育委员发现在学校附近有甲、乙两家商店都在出售相同品牌的乒乓球拍和乒乓球,乒乓球拍每副售价100元,乒乓球每盒售价25元.经过体育委员的洽谈,甲商店给出每买一副乒乓球拍送一盒乒乓球的优惠;乙商店给出乒乓球拍和乒乓球全部九折的优惠.
(1)若这个班计划购买6盒乒乓球,则在甲商店付款 元,在乙商店付款 元;
(2)当这个班购买多少盒乒乓球时,在甲、乙两家商店付款相同?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校假期由校长带领该校“三好学生”去旅游,甲旅行社说“若校长买全票一张,则学生半价.”乙旅行社说“全部人六折优惠”若全票价是1200元,则:
(1)若学生人数是20人,甲、乙旅行社收费分别是多少?
(2)当学生人数的多少时,两家旅行社的收费一样?
-
科目: 来源: 题型:
查看答案和解析>>【题目】程大位是我国明朝商人,珠算发明家,他60岁时完成的《直指算法综宗》是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法,书中有如下问题:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚得几丁,意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,大、小和尚各有多少人,则小和尚有__________人.
-
科目: 来源: 题型:
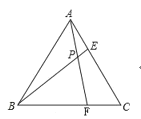
查看答案和解析>>【题目】如图,在边长为6的等边三角形ABC中,点E、F分别是边AC、BC上的动点,连接AF、BE,交于点P,若始终保持AE=CF,当点E从点A运动到点C时,则点P运动的路径长__________.
相关试题

