【题目】已知如图1,在△ABC中,∠ACB=90°,BC=AC,点D在AB上,DE⊥AB交BC于E,点F是AE的中点
(1)写出线段FD与线段FC的关系并证明;
(2)如图2,将△BDE绕点B逆时针旋转α(0°<α<90°),其它条件不变,线段FD与线段FC的关系是否变化,写出你的结论并证明;
(3)将△BDE绕点B逆时针旋转一周,如果BC=4,BE=2![]() ,直接写出线段BF的范围.
,直接写出线段BF的范围.

参考答案:
【答案】(1)结论:FD=FC,DF⊥CF.理由见解析;(2)结论不变.理由见解析;(3)![]() ≤BF
≤BF![]() .
.
【解析】
(1)结论:FD=FC,DF⊥CF.由直角三角形斜边中线定理即可证明;
(2)如图2中,延长AC到M使得CM=CA,延长ED到N,使得DN=DE,连接BN、BM.EM、AN,延长ME交AN于H,交AB于O.想办法证明△ABN≌△MBE,推出AN=EM,再利用三角形中位线定理即可解决问题;
(3)分别求出BF的最大值、最小值即可解决问题;
解:(1)结论:FD=FC,DF⊥CF.
理由:如图1中,
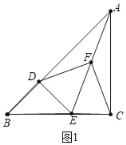
∵∠ADE=∠ACE=90°,AF=FE,
∴DF=AF=EF=CF,
∴∠FAD=∠FDA,∠FAC=∠FCA,
∴∠DFE=∠FDA+∠FAD=2∠FAD,∠EFC=∠FAC+∠FCA=2∠FAC,
∵CA=CB,∠ACB=90°,
∴∠BAC=45°,
∴∠DFC=∠EFD+∠EFC=2(∠FAD+∠FAC)=90°,
∴DF=FC,DF⊥FC.
(2)结论不变.
理由:如图2中,延长AC到M使得CM=CA,延长ED到N,使得DN=DE,连接BN、BM.EM、AN,延长ME交AN于H,交AB于O.
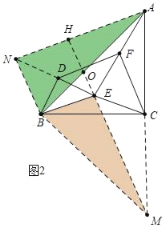
∵BC⊥AM,AC=CM,
∴BA=BM,同法BE=BN,
∵∠ABM=∠EBN=90°,
∴∠NBA=∠EBM,
∴△ABN≌△MBE,
∴AN=EM,∴∠BAN=∠BME,
∵AF=FE,AC=CM,
∴CF=![]() EM,FC∥EM,同法FD=
EM,FC∥EM,同法FD=![]() AN,FD∥AN,
AN,FD∥AN,
∴FD=FC,
∵∠BME+∠BOM=90°,∠BOM=∠AOH,
∴∠BAN+∠AOH=90°,
∴∠AHO=90°,
∴AN⊥MH,FD⊥FC.
(3)![]() .
.
当点![]() 落在
落在![]() 上时,
上时,![]() 取得最大值,
取得最大值,
如图5所示,∵![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,
∵![]() 是
是![]() 的中点,∴
的中点,∴![]() ,
,
又![]() ,
,
∴![]() ,
,
即![]() 的最大值为
的最大值为![]() .
.
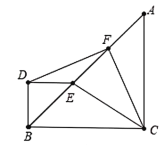
图5
当点![]() 落在
落在![]() 延长线上时,
延长线上时,![]() 取得长最小值,
取得长最小值,
如图6所示,∵![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,
∵![]() 是
是![]() 的中点,∴
的中点,∴![]() ,
,
又![]() ,
,
∴![]() ,
,
即![]() 的最小值为
的最小值为![]() .
.
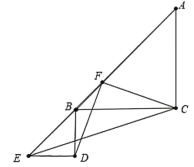
图6
综上所述,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=kx+b经过点A(5,0),B(1,4).

(1)求直线AB的解析式;
(2)若直线y=2x﹣4与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式2x﹣4≥kx+b的解集.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点E在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF,M、N分别是DC、DF的中点,连接MN.若AB=7,BE=5,则MN=_______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙C过原点O,且与两坐标轴分别交于点A、B,点A的坐标为(0,2),M是第三象限内⊙C上一点,∠BMO=120°,则圆心C的坐标为( )

A. (1,1) B. (1,
 ) C. (2,1) D. (﹣
) C. (2,1) D. (﹣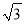 ,1)
,1) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B的坐标是(0,1),AB⊥y轴,垂足为B,点A在直线y=
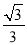 x,将△ABO绕点A顺时针旋转到△AB1O1的位置,使点B的对应点B1落在直线y=
x,将△ABO绕点A顺时针旋转到△AB1O1的位置,使点B的对应点B1落在直线y=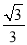 x上,再将△AB1O1绕点B1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=
x上,再将△AB1O1绕点B1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=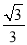 x上,依次进行下去…,则点O100的纵坐标是_____.
x上,依次进行下去…,则点O100的纵坐标是_____.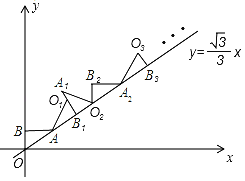
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是正方形,点E、F分别是BC、CD边的中点,连结AE、BF交于点P,连结DP.
(1)求证:AE⊥BF.
(2)求证:PD=AB.

-
科目: 来源: 题型:
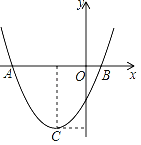
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点C的坐标为(﹣1,﹣3),与x轴交于A(﹣3,0)、B(1,0),根据图象回答下列问题:
(1)写出方程ax2+bx+c=0的根;
(2)写出不等式ax2+bx+c>0的解集;
(3)若方程ax2+bx+c=k有实数根,写出实数k的取值范围.
相关试题

