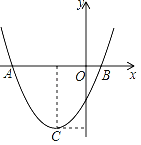
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点C的坐标为(﹣1,﹣3),与x轴交于A(﹣3,0)、B(1,0),根据图象回答下列问题:
(1)写出方程ax2+bx+c=0的根;
(2)写出不等式ax2+bx+c>0的解集;
(3)若方程ax2+bx+c=k有实数根,写出实数k的取值范围.
参考答案:
【答案】(1)x1=-3、x2=1;(2)x<-3或x>1;(3)k≥-3.
【解析】试题分析:
(1)一元二次方程ax2+bx+c=0的根是二次函数y=ax2+bx+c(a≠0)的图象与x轴交点
的横坐标可得答案;
(2)由不等式ax2+bx+c>0的解集是抛物线位于横轴之上的部分图象所对应的自变量的取值可得解集;
(3)由方程ax2+bx+c=k有实数根,则抛物线y=ax2+bx+c(a≠0)与直线y=k有交点,结合抛物线y=ax2+bx+c(a≠0)的顶点坐标为(﹣1,﹣3)可得答案;
试题解析:
(1)∵方程ax2+bx+c=0的根是二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标,
∴方程ax2+bx+c=0的根为x1=-3、x2=1;
(2)不等式ax2+bx+c>0的解集是抛物线在x轴上方部分图象对应的x的范围,
∴不等式ax2+bx+c>0的解集为x<-3或x>1;
(3)∵方程ax2+bx+c=k有实数根,
∴抛物线y=ax2+bx+c与直线y=k有交点,
由函数图象知k≥-3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图1,在△ABC中,∠ACB=90°,BC=AC,点D在AB上,DE⊥AB交BC于E,点F是AE的中点
(1)写出线段FD与线段FC的关系并证明;
(2)如图2,将△BDE绕点B逆时针旋转α(0°<α<90°),其它条件不变,线段FD与线段FC的关系是否变化,写出你的结论并证明;
(3)将△BDE绕点B逆时针旋转一周,如果BC=4,BE=2
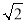 ,直接写出线段BF的范围.
,直接写出线段BF的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B的坐标是(0,1),AB⊥y轴,垂足为B,点A在直线y=
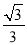 x,将△ABO绕点A顺时针旋转到△AB1O1的位置,使点B的对应点B1落在直线y=
x,将△ABO绕点A顺时针旋转到△AB1O1的位置,使点B的对应点B1落在直线y=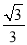 x上,再将△AB1O1绕点B1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=
x上,再将△AB1O1绕点B1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=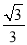 x上,依次进行下去…,则点O100的纵坐标是_____.
x上,依次进行下去…,则点O100的纵坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知四边形ABCD是正方形,点E、F分别是BC、CD边的中点,连结AE、BF交于点P,连结DP.
(1)求证:AE⊥BF.
(2)求证:PD=AB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件,其中甲种奖品每件40元,乙种奖品每件30元.
(1)如果购买甲、乙两种奖品共花费了650元,求甲、乙两种奖品各购买了多少件;
(2)如果购买乙种奖品的件数不超过甲种奖品件数的2倍,总花费不超过680元,求该公司有哪几种不同的购买方案.
-
科目: 来源: 题型:
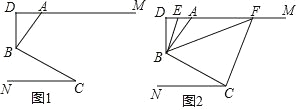
查看答案和解析>>【题目】如图 1,AM∥CN,点 B 为平面内一点,AB⊥BC 于 B,过 B 作 BD⊥ AM.
(1)求证:∠ABD=∠C;
(2)如图 2,在(1)问的条件下,分别作∠ABD、∠DBC 的平分线交 DM 于 E、F,若∠BFC=1.5∠ABF,∠FCB=2.5∠BCN,
①求证:∠ABF=∠AFB;
②求∠CBE 的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在括号内填写理由.
如图,已知∠B+∠BCD=180°,∠B=∠D.
求证:∠E=∠DFE.

证明:∵∠B+∠BCD=180°(已知),
∴AB∥CD(______________________).
∴∠B=_______(_____________________).
又∵∠B=∠D(已知),
∴∠DCE=∠D(_____________________).
∴AD∥BE(_____________________).
∴∠E=∠DFE(_____________________).
相关试题

