【题目】如图,已知四边形ABCD是正方形,点E、F分别是BC、CD边的中点,连结AE、BF交于点P,连结DP.
(1)求证:AE⊥BF.
(2)求证:PD=AB.

参考答案:
【答案】(1)见解析;(2)见解析
【解析】
(1)根据“边角边”证明![]() ,得到
,得到![]() ,
,![]() ;利用等量代换,得到
;利用等量代换,得到![]() ;再根据三角形内角和定理,可得
;再根据三角形内角和定理,可得![]() ,即可得证
,即可得证![]() .
.
(2)如图,延长![]() 交
交![]() 延长线于
延长线于![]() .根据“角边角”证明
.根据“角边角”证明![]() ,得到
,得到![]() ,即得到点
,即得到点![]() 为
为![]() 的中点;根据直角三角形斜边上的中线的性质,可得在直角三角形
的中点;根据直角三角形斜边上的中线的性质,可得在直角三角形![]() 中,
中,![]() ,即可得
,即可得![]() .
.
(1)∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,
∵点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 边的中点,
边的中点,
∴![]() ,
,
∴在![]() 和
和![]() 中,
中,
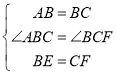
∴![]() ,
,
∴![]() ,
,![]() ,
,
又∵在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)如图,延长![]() 交
交![]() 延长线于
延长线于![]() ,则
,则![]() ,
,
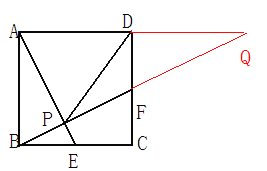
∵点![]() 是
是![]() 边的中点,∴
边的中点,∴![]() ,
,
∴在![]() 和
和![]() 中,
中,
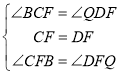
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴点![]() 为
为![]() 的中点,
的中点,
∵由(1)得![]() ,
,
∴![]() 为直角三角形,
为直角三角形,
∴![]() ,
,
又![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙C过原点O,且与两坐标轴分别交于点A、B,点A的坐标为(0,2),M是第三象限内⊙C上一点,∠BMO=120°,则圆心C的坐标为( )

A. (1,1) B. (1,
 ) C. (2,1) D. (﹣
) C. (2,1) D. (﹣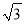 ,1)
,1) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图1,在△ABC中,∠ACB=90°,BC=AC,点D在AB上,DE⊥AB交BC于E,点F是AE的中点
(1)写出线段FD与线段FC的关系并证明;
(2)如图2,将△BDE绕点B逆时针旋转α(0°<α<90°),其它条件不变,线段FD与线段FC的关系是否变化,写出你的结论并证明;
(3)将△BDE绕点B逆时针旋转一周,如果BC=4,BE=2
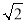 ,直接写出线段BF的范围.
,直接写出线段BF的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B的坐标是(0,1),AB⊥y轴,垂足为B,点A在直线y=
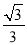 x,将△ABO绕点A顺时针旋转到△AB1O1的位置,使点B的对应点B1落在直线y=
x,将△ABO绕点A顺时针旋转到△AB1O1的位置,使点B的对应点B1落在直线y=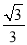 x上,再将△AB1O1绕点B1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=
x上,再将△AB1O1绕点B1顺时针旋转到△A1B1O2的位置,使点O1的对应点O2落在直线y=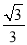 x上,依次进行下去…,则点O100的纵坐标是_____.
x上,依次进行下去…,则点O100的纵坐标是_____.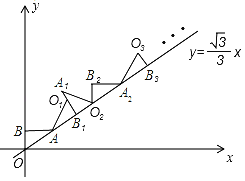
-
科目: 来源: 题型:
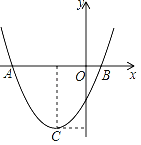
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的顶点C的坐标为(﹣1,﹣3),与x轴交于A(﹣3,0)、B(1,0),根据图象回答下列问题:
(1)写出方程ax2+bx+c=0的根;
(2)写出不等式ax2+bx+c>0的解集;
(3)若方程ax2+bx+c=k有实数根,写出实数k的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司为奖励在趣味运动会上取得好成绩的员工,计划购买甲、乙两种奖品共20件,其中甲种奖品每件40元,乙种奖品每件30元.
(1)如果购买甲、乙两种奖品共花费了650元,求甲、乙两种奖品各购买了多少件;
(2)如果购买乙种奖品的件数不超过甲种奖品件数的2倍,总花费不超过680元,求该公司有哪几种不同的购买方案.
-
科目: 来源: 题型:
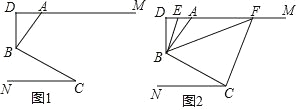
查看答案和解析>>【题目】如图 1,AM∥CN,点 B 为平面内一点,AB⊥BC 于 B,过 B 作 BD⊥ AM.
(1)求证:∠ABD=∠C;
(2)如图 2,在(1)问的条件下,分别作∠ABD、∠DBC 的平分线交 DM 于 E、F,若∠BFC=1.5∠ABF,∠FCB=2.5∠BCN,
①求证:∠ABF=∠AFB;
②求∠CBE 的度数.
相关试题

