搜索
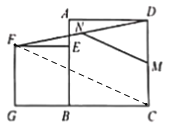
【题目】如图，已知点E在正方形ABCD的边AB上，以BE为边向正方形ABCD外部作正方形BEFG，连接DF，M、N分别是DC、DF的中点，连接MN.若AB=7，BE=5，则MN=_______.
参考答案：
【答案】
【解析】
连接FC，根据三角形中位线定理可得FC=2MN，继而根据四边形ABCD，四边形EFGB是正方形，推导得出G、B、C三点共线，然后再根据勾股定理可求得FC的长，继而可求得答案.
连接FC，∵M、N分别是DC、DF的中点，
∴FC=2MN，
∵四边形ABCD，四边形EFGB是正方形，
∴∠FGB=90°，∠ABG=∠ABC=90°，FG=BE=5，BC=AB=7，
∴∠GBC=∠ABG+∠ABC=180°，
即G、B、C三点共线，
∴GC=GB+BC=5+7=12，
∴FC=
=13，
∴MN=，
故答案为：.
-
科目： 来源： 题型：
查看答案和解析>>【题目】小明参加某网店的“翻牌抽奖”活动．如图，4张牌分别对应价值5，10，15，20(单位：元)的4件奖品．
(1)如果随机翻1张牌，求抽中20元奖品的概率；
(2)如果随机翻两张牌，且第一次翻过的牌不再参加下次翻牌，求所获奖品总值不低于30元的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,根据图中信息解答下列问题:
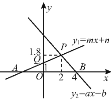
(1)关于x的不等式ax+b>0的解集是 .
(2)关于x的不等式mx+n<1的解集是 .
(3)当x为何值时,y1≤y2?
(4)当x为何值时,0<y2<y1?
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y=kx+b经过点A（5，0），B（1，4）．
（1）求直线AB的解析式；
（2）若直线y=2x﹣4与直线AB相交于点C，求点C的坐标；
（3）根据图象，写出关于x的不等式2x﹣4≥kx+b的解集．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，⊙C过原点O，且与两坐标轴分别交于点A、B，点A的坐标为（0，2），M是第三象限内⊙C上一点，∠BMO=120°，则圆心C的坐标为（ ）
A. （1，1） B. （1，
） C. （2，1） D. （﹣
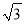，1） -
科目： 来源： 题型：
查看答案和解析>>【题目】已知如图1，在△ABC中，∠ACB＝90°，BC＝AC，点D在AB上，DE⊥AB交BC于E，点F是AE的中点
（1）写出线段FD与线段FC的关系并证明；
（2）如图2，将△BDE绕点B逆时针旋转α（0°＜α＜90°），其它条件不变，线段FD与线段FC的关系是否变化，写出你的结论并证明；
（3）将△BDE绕点B逆时针旋转一周，如果BC＝4，BE＝2
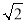，直接写出线段BF的范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点B的坐标是（0，1），AB⊥y轴，垂足为B，点A在直线y=
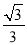x，将△ABO绕点A顺时针旋转到△AB1O1的位置，使点B的对应点B1落在直线y=
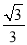x上，再将△AB1O1绕点B1顺时针旋转到△A1B1O2的位置，使点O1的对应点O2落在直线y=
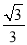x上，依次进行下去…，则点O100的纵坐标是_____．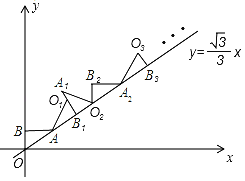
相关试题
