【题目】如图 ,已知B C=90 ,AEED,ABCE ,点F是AD的中点.说明EF与AD垂直的理由.
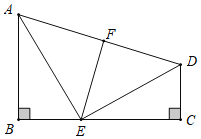
解:因为 AEED (已知),
所以AED=90 (垂直的意义).
因为AECBBAE ( ),
即AEDDECBBAE .
又因为B=90 (已知),
所以BAECED (等式性质).
在△ ABE 与△ ECD 中,
BC(已知),ABEC(已知),BAECED,
所以△ ABE≌△ECD ( ),
得 ( 全等三角形的对应边相等),
所以△AED 是等腰三角形.
因为 (已知),
所以 EFAD ( ).
参考答案:
【答案】见解析.
【解析】
证出∠BAE=∠CED,证明△ABE ≌△ECD,得出AE=DE,可知△AED是等腰三角形,由等腰三角形的三线合一性质即可得出结论.
因为AE ED(已知),
所以AED=90(垂直的意义),
因为AEC B BAE( 三角形的一个外角等于与它不相邻的两个内角的和),
即AED DEC B BAE,
又因为B=90(已知),
所以BAE CED(等式性质).
在△ABE与△ECD 中,
B C(已知),AB EC(已知),BAE CED,
所以△ABE≌△ECD(ASA).
得AE ED(全等三角形对应边相等).
所以△AED 是等腰三角形.
因为点F是AD的中点(已知),
所以EF AD(等腰三角形的三线合一).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFMN的一边MN在边BC上,顶点E、F分别在AB、AC上,其中BC=24cm,高AD=12cm.
(1)求证:△AEF∽△ABC:
(2)求正方形EFMN的边长.

-
科目: 来源: 题型:
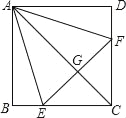
查看答案和解析>>【题目】如图,正方形ABCD中,点E,F分别在BC,CD上,三角形AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②AG=2GC,③BE+DF=EF,④S△CEF=2S△ABE正确的有_____(只填序号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
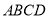 中,
中,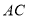 为对角线,点
为对角线,点 为
为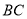 边上一动点,连结
边上一动点,连结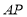 ,过点
,过点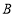 作
作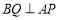 ,垂足为
,垂足为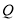 ,连结
,连结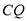 .
.(1)证明:
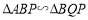 ;
;(2)当点
 为
为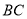 的中点时,若
的中点时,若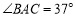 ,求
,求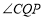 的度数;
的度数;(3)当点
 运动到与点
运动到与点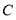 重合时,延长
重合时,延长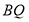 交
交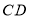 于点
于点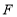 ,若
,若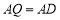 ,则
,则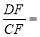 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,连接AE.
求证:(1)BF=DF;
(2)若AB=6,AD=8,求BF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)某学校“智慧方园”数学社团遇到这样一个题目:
如图1,在
 中,点
中,点 在线段
在线段 上,
上, ,
, ,
, ,
, ,求
,求 的长.
的长.经过社团成员讨论发现,过点
 作
作 ,交
,交 的延长线于点
的延长线于点 ,通过构造
,通过构造 就可以解决问题(如图
就可以解决问题(如图 .
.请回答:

 ,
, .
.(2)请参考以上解决思路,解决问题:
如图3,在四边形
 中,对角线
中,对角线 与
与 相交于点
相交于点 ,
, ,
, ,
, ,
, ,求
,求 的长.
的长.
-
科目: 来源: 题型:
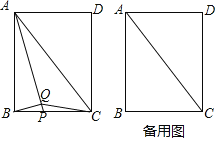
查看答案和解析>>【题目】如图1,点
 是正方形
是正方形 的中心,点
的中心,点 是
是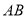 边上一动点,在
边上一动点,在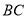 上截取
上截取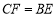 ,连结
,连结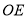 ,
,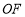 .初步探究:在点
.初步探究:在点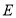 的运动过程中:
的运动过程中:(1)猜想线段
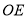 与
与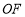 的关系,并说明理由.
的关系,并说明理由.深入探究:
(2)如图2,连结
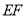 ,过点
,过点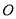 作
作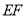 的垂线交
的垂线交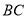 于点
于点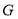 .交
.交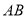 的延长线于点
的延长线于点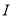 .延长
.延长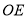 交
交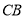 的延长线于点
的延长线于点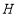 .
.①直接写出
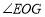 的度数.
的度数.②若
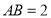 ,请探究
,请探究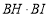 的值是否为定值,若是,请求出其值;反之,请说明理由
的值是否为定值,若是,请求出其值;反之,请说明理由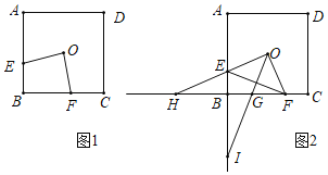
相关试题

