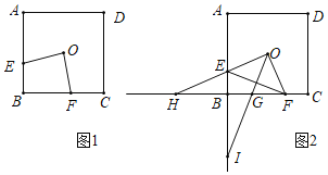
【题目】如图1,点![]() 是正方形
是正方形![]() 的中心,点
的中心,点![]() 是
是![]() 边上一动点,在
边上一动点,在![]() 上截取
上截取![]() ,连结
,连结![]() ,
,![]() .初步探究:在点
.初步探究:在点![]() 的运动过程中:
的运动过程中:
(1)猜想线段![]() 与
与![]() 的关系,并说明理由.
的关系,并说明理由.
深入探究:
(2)如图2,连结![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() .交
.交![]() 的延长线于点
的延长线于点![]() .延长
.延长![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
①直接写出![]() 的度数.
的度数.
②若![]() ,请探究
,请探究![]() 的值是否为定值,若是,请求出其值;反之,请说明理由
的值是否为定值,若是,请求出其值;反之,请说明理由
参考答案:
【答案】(1)EO⊥FO,EO=FO;理由见解析;(2)①![]() ;②
;②![]() =2
=2
【解析】
(1)由正方形的性质可得BO=CO,∠ABO=∠ACB=45°,∠BOC=90°,由“SAS”可证△BEO≌△CFO,可得OE=OF,∠BOE=∠COF,可证EO⊥FO;
(2)①由等腰直角三角形的性质可得∠EOG的度数;
②由∠EOF=∠ABF=90°,可得点E,点O,点F,点B四点共圆,可得∠EOB=∠BFE,通过证明△BOH∽△BIO,可得![]() ,即可得结论.
,即可得结论.
解:(1)OE=OF,OE⊥OF,连接AC,BD,
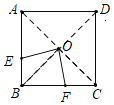
∵点O是正方形ABCD的中心
∴点O是AC,BD的交点
∴BO=CO,∠ABO=∠ACB=45°,∠BOC=90°
∵CF=BE,∠ABO=∠ACB,BO=CO,
∴△BEO≌△CFO(SAS)
∴OE=OF,∠BOE=∠COF
∵∠COF+∠BOF=90°,
∴∠BOE+∠BOF=90°
∴∠EOF=90°,
∴EO⊥FO.
(2)
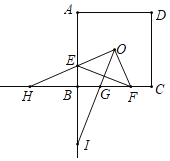
①∵OE=OF,OE⊥OF,
∴△EOF是等腰直角三角形,OG⊥EF
∴∠EOG=45°
②BHBI的值是定值,
理由如下:
如图,连接DB,
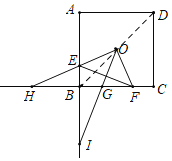
∵AB=BC=CD=2
∴BD=2![]() ,
,
∴BO=![]()
∵∠AOB=∠COB=45°,∠HBE=∠GBI=90°
∴∠HBO=∠IBO=135°
∵∠EOF=∠ABF=90°
∴点E,点O,点F,点B四点共圆
∴∠EOB=∠BFE,
∵EF⊥OI,AB⊥HF
∴∠BEF+∠BFE=90°,∠BEF+∠EIO=90°
∴∠BFE=∠BIO,
∴∠BOE=∠BIO,且∠HBO=∠IBO
∴△BOH∽△BIO
∴![]()
∴BHBI=BO2=2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 ,已知B C=90 ,AEED,ABCE ,点F是AD的中点.说明EF与AD垂直的理由.
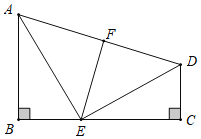
解:因为 AEED (已知),
所以AED=90 (垂直的意义).
因为AECBBAE ( ),
即AEDDECBBAE .
又因为B=90 (已知),
所以BAECED (等式性质).
在△ ABE 与△ ECD 中,
BC(已知),ABEC(已知),BAECED,
所以△ ABE≌△ECD ( ),
得 ( 全等三角形的对应边相等),
所以△AED 是等腰三角形.
因为 (已知),
所以 EFAD ( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,连接AE.
求证:(1)BF=DF;
(2)若AB=6,AD=8,求BF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)某学校“智慧方园”数学社团遇到这样一个题目:
如图1,在
 中,点
中,点 在线段
在线段 上,
上, ,
, ,
, ,
, ,求
,求 的长.
的长.经过社团成员讨论发现,过点
 作
作 ,交
,交 的延长线于点
的延长线于点 ,通过构造
,通过构造 就可以解决问题(如图
就可以解决问题(如图 .
.请回答:

 ,
, .
.(2)请参考以上解决思路,解决问题:
如图3,在四边形
 中,对角线
中,对角线 与
与 相交于点
相交于点 ,
, ,
, ,
, ,
, ,求
,求 的长.
的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 中,
中, ,
, ,
, 是
是 上一点,且
上一点,且 ,过点
,过点 分别作
分别作 ,
, ,垂足分别是
,垂足分别是 ,下列结论:①
,下列结论:① ;②
;② 是
是 的中点;③
的中点;③ 垂直平分
垂直平分 ;④
;④ ;其中正确的个数为( )
;其中正确的个数为( )
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
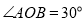 ,点
,点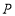 为
为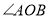 内一点,
内一点,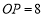 ,点
,点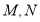 分别在射线
分别在射线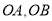 上,当
上,当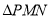 的周长最小时,下列结论:①
的周长最小时,下列结论:①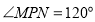 ;②
;②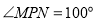 ;③
;③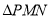 的周长最小值为24;④
的周长最小值为24;④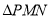 的周长最小值为8;其中正确的序号为__________.
的周长最小值为8;其中正确的序号为__________.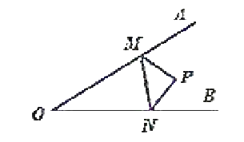
相关试题

