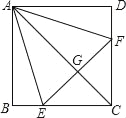
【题目】如图,正方形ABCD中,点E,F分别在BC,CD上,三角形AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②AG=2GC,③BE+DF=EF,④S△CEF=2S△ABE正确的有_____(只填序号).
参考答案:
【答案】①④.
【解析】分析:先通过证明Rt△ABE≌Rt△ADF可对①进行判断;再证明AG垂直平分EF得到CG=![]() EF,即EF=2CG,则利用EF>AG可对②进行判断;由于∠EAG=30°,∠BAE=15°,则可判断BE≠EG,然后利用BE+DF=2BE,EF=2EG可对③进行判断;延长CB到F′使BF′=DF,作EH⊥AF′于H,如图,易得△ABF′≌△ABE,∠EAF′=30°,设CG=x,则EG=GF=x,AE=2x,所以EH=x,然后根据三角形面积公式可对④进行判断.
EF,即EF=2CG,则利用EF>AG可对②进行判断;由于∠EAG=30°,∠BAE=15°,则可判断BE≠EG,然后利用BE+DF=2BE,EF=2EG可对③进行判断;延长CB到F′使BF′=DF,作EH⊥AF′于H,如图,易得△ABF′≌△ABE,∠EAF′=30°,设CG=x,则EG=GF=x,AE=2x,所以EH=x,然后根据三角形面积公式可对④进行判断.
详解:∵△AEF为等边三角形,
∴AE=AF,
∵四边形ABCD为正方形,
∴AB=AD,∠B=∠D=∠BAD=90°,
在Rt△ABE和Rt△ADF中
![]()
∴Rt△ABE≌Rt△ADF,
∴BE=DF,所以①正确;
∠BAE=∠DAF,
∵AC平分∠BAD,
∴∠BAG=∠FAG,
∴AG垂直平分EF,
∴CG=![]() EF,即EF=2CG,
EF,即EF=2CG,
而EF>AG,
∴AG<2CG,所以②错误;
∵∠EAG=30°,∠BAE=15°,
∴BE≠EG,
∴BE+DF=2BE,EF=2EG,
∴BE+DF≠EF,所以③错误;
延长CB到F′使BF′=DF,作EH⊥AF′于H,如图,
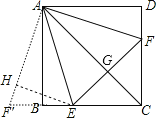
易得△ABF′≌△ABE,
∴∠EAF′=30°,
设CG=x,则EG=GF=x,AE=2x,
∴EH=x,
∴S△AF′E=![]() 2xx=x2,S△CEF=
2xx=x2,S△CEF=![]() x2x=x2,
x2x=x2,
∴S△CEF=2S△ABE,所以④正确.
故答案为①④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数
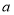 、b在数轴上的位置如图所示,
、b在数轴上的位置如图所示, 
(1) a+b 0 , a-b 0; (填“>”、“=”或“<”)
(2) 化简:|a|-|b|+|a-b|
(3)在数轴上表示a+b与a-b;并把
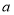 、b、0、a+b、a-b按从小到的顺序用“<”连接起来。
、b、0、a+b、a-b按从小到的顺序用“<”连接起来。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
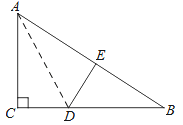
(1)求证:△BDE∽△BAC;
(2)已知AC=6,BC=8,求线段AD的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFMN的一边MN在边BC上,顶点E、F分别在AB、AC上,其中BC=24cm,高AD=12cm.
(1)求证:△AEF∽△ABC:
(2)求正方形EFMN的边长.

-
科目: 来源: 题型:
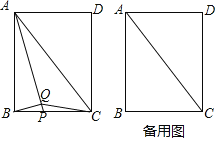
查看答案和解析>>【题目】如图,在矩形
 中,
中,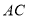 为对角线,点
为对角线,点 为
为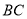 边上一动点,连结
边上一动点,连结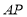 ,过点
,过点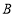 作
作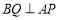 ,垂足为
,垂足为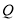 ,连结
,连结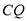 .
.(1)证明:
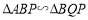 ;
;(2)当点
 为
为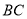 的中点时,若
的中点时,若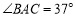 ,求
,求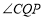 的度数;
的度数;(3)当点
 运动到与点
运动到与点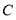 重合时,延长
重合时,延长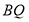 交
交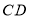 于点
于点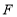 ,若
,若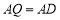 ,则
,则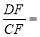 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 ,已知B C=90 ,AEED,ABCE ,点F是AD的中点.说明EF与AD垂直的理由.
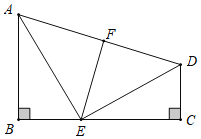
解:因为 AEED (已知),
所以AED=90 (垂直的意义).
因为AECBBAE ( ),
即AEDDECBBAE .
又因为B=90 (已知),
所以BAECED (等式性质).
在△ ABE 与△ ECD 中,
BC(已知),ABEC(已知),BAECED,
所以△ ABE≌△ECD ( ),
得 ( 全等三角形的对应边相等),
所以△AED 是等腰三角形.
因为 (已知),
所以 EFAD ( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,连接AE.
求证:(1)BF=DF;
(2)若AB=6,AD=8,求BF的长.

相关试题

