【题目】在⊙O中,AB为直径,∠ACD=45°,已知AC=7,BC=5,则CD =_______
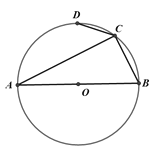
参考答案:
【答案】![]() 或
或![]()
【解析】
分情况讨论,过点A作AM⊥CD,过点B作BN⊥CD,连接AD,BD,通过证明△MAC,△NBC,△ABD均为等腰直角三角形和△MAD≌△NDB求解.
解:如图:过点A作AM⊥CD,过点B作BN⊥CD,连接AD,BD
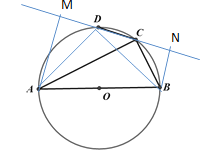
∵![]() 且AB是圆的直径
且AB是圆的直径
∴△MAC,△NBC,△ABD均为等腰直角三角形
∴AD=BD
∵AM⊥CD, BN⊥CD
∴![]()
又∵![]()
∴![]()
∴△MAD≌△NDB
∴DN=AM
又∵△MAC,△NBC均为等腰直角三角形
∴![]() ,
, ![]()
∴![]() ;
;
如图:过点A作AM⊥CD,过点B作BN⊥CD,连接AD,BD
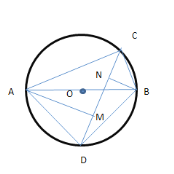
同理可证,此时![]()
故答案为:![]() 或
或![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O的半径为1,弦AB=1,点P为优弧AB上一动点,AC⊥AP交直线PB于点C,则△ABC的最大面积是( )
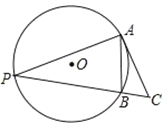
A.
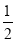 B.
B.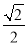 C.
C.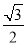 D.
D.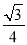
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,半径OA⊥弦BC于点H,点D在优弧BC上
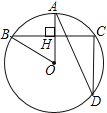
(1)若∠AOB=50°,求∠ADC的度数;
(2)若BC=8,AH=2,求⊙O的半径.
-
科目: 来源: 题型:
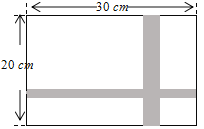
查看答案和解析>>【题目】如图,要设计一副宽20 cm、长30 cm的图案,其中有一横一竖的彩条,横、竖彩条的宽度之比为2∶3.如果要彩条所占面积是图案面积的19%,问横、竖彩条的宽度各为多少cm?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形
 中,
中,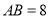 ,
,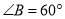 ,
,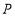 是
是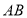 上一点,
上一点,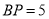 ,
,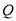 是
是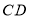 边上一动点,将四边形
边上一动点,将四边形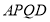 沿直线
沿直线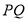 折叠,
折叠,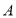 的对应点
的对应点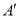 .当
.当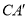 的长度最小时,则
的长度最小时,则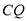 的长为_______
的长为_______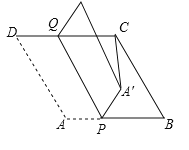
-
科目: 来源: 题型:
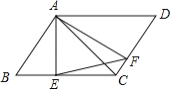
查看答案和解析>>【题目】如图,四边形
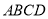 是平行四边形,
是平行四边形, ,
, ,垂足分别为
,垂足分别为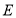 、
、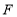 ,连接
,连接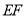 .
.求证:(1)
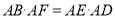 ;(2)
;(2)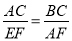 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中以AB为直径作⊙O,分别交边AC、BC于D、E,过D作DF⊥BC于F,且D为弧AE的中点.
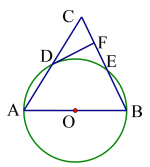
(1)求证:DF为⊙O的切线;
(2)若
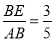 且AD=
且AD=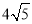 时,求⊙O的半径
时,求⊙O的半径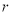 .
.
相关试题

