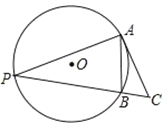
【题目】如图,O的半径为1,弦AB=1,点P为优弧AB上一动点,AC⊥AP交直线PB于点C,则△ABC的最大面积是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
参考答案:
【答案】D
【解析】
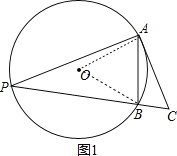
连结OA、OB,如图1,由OA=OB=AB=1可判断△OAB为等边三角形,则∠AOB=60°,根据圆周角定理得∠APB=![]() ∠AOB=30°,由于AC⊥AP,所以∠C=60°,因为AB=1,则要使△ABC的最大面积,点C到AB的距离要最大;由∠ACB=60°,可根据圆周角定理判断点C在⊙D上,且∠ADB=120°,如图2,于是当点C优弧AB的中点时,点C到AB的距离最大,此时△ABC为等边三角形,从而得到△ABC的最大面积.
∠AOB=30°,由于AC⊥AP,所以∠C=60°,因为AB=1,则要使△ABC的最大面积,点C到AB的距离要最大;由∠ACB=60°,可根据圆周角定理判断点C在⊙D上,且∠ADB=120°,如图2,于是当点C优弧AB的中点时,点C到AB的距离最大,此时△ABC为等边三角形,从而得到△ABC的最大面积.
解:连结OA、OB,作△ABC的外接圆D,如图1,
∵OA=OB=1,AB=1,
∴△OAB为等边三角形,
∴∠AOB=60°,
∴∠APB=![]() ∠AOB=30°,
∠AOB=30°,
∵AC⊥AP,
∴∠C=60°,
∵AB=1,要使△ABC的最大面积,则点C到AB的距离最大,
∵∠ACB=60°,点C在⊙D上,
∴∠ADB=120°,
如图2,
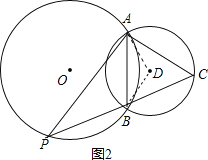
当点C优弧AB的中点时,点C到AB的距离最大,此时△ABC为等边三角形,且面积为![]() ,
,
∴△ABC的最大面积为![]() .
.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且AC=CF,∠CBF=∠CFB.
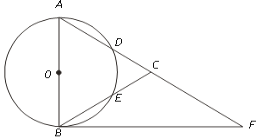
(1)求证:直线BF是⊙O的切线;
(2)若点D,点E分别是弧AB的三等分点,当AD=5时,求BF的长和扇形DOE的面积;
(3)在(2)的条件下,如果以点C为圆心,r为半径的圆上总存在不同的两点到点O的距离为5,则r的取值范围为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】小东根据学习函数的经验,对函数
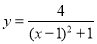 的图像与性质进行了探究,下面是小东的探究过程,请补充完整,并解决相关问题:
的图像与性质进行了探究,下面是小东的探究过程,请补充完整,并解决相关问题:(1)函数
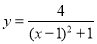 的自变量x的取值范围是__________________
的自变量x的取值范围是__________________(2)如表示y与x的几组对应值:
x
…
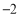
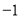
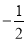
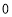
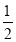
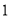
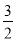
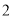
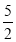
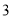
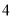
…
y
…
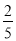
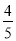
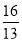
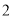
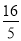
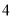
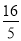
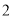
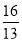
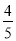
m
…
表中m的值为____________
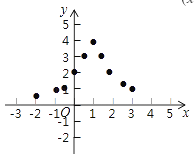
(3)如图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出函数
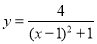 的大致图像;
的大致图像;(4)结合函数图像,请写出函数
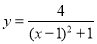 的2条性质:
的2条性质:①__________________________________________________________________________
②__________________________________________________________________________
(5)解决问题:如果函数
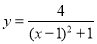 与直线
与直线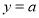 的交点有2个,那么a的取值范围是_______________________
的交点有2个,那么a的取值范围是_______________________(6)
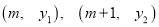 在函数图像上,若
在函数图像上,若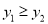 ,则m的取值范围______________
,则m的取值范围______________ -
科目: 来源: 题型:
查看答案和解析>>【题目】荆州市某水产养殖户进行小龙虾养殖.已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价p(元/千克)与时间第t(天)之间的函数关系为:
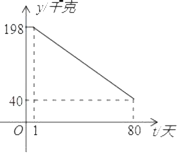
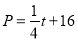 (1≤t≤80,t为整数),日销售量y(千克)与时间第t(天)之间的函数关系如图所示:
(1≤t≤80,t为整数),日销售量y(千克)与时间第t(天)之间的函数关系如图所示:(1)求日销售量y与时间t的函数关系式?
(2)哪一天的日销售利润最大?最大利润是多少?
(3)在实际销售的前40天中,该养殖户决定每销售1千克小龙虾,就捐赠m(m<7)元给村里的特困户.在这前40天中,每天扣除捐赠后的日销售利润随时间t的增大而增大,求m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,半径OA⊥弦BC于点H,点D在优弧BC上
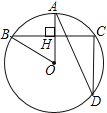
(1)若∠AOB=50°,求∠ADC的度数;
(2)若BC=8,AH=2,求⊙O的半径.
-
科目: 来源: 题型:
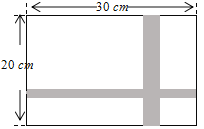
查看答案和解析>>【题目】如图,要设计一副宽20 cm、长30 cm的图案,其中有一横一竖的彩条,横、竖彩条的宽度之比为2∶3.如果要彩条所占面积是图案面积的19%,问横、竖彩条的宽度各为多少cm?
-
科目: 来源: 题型:
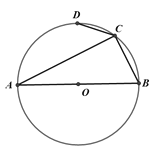
查看答案和解析>>【题目】在⊙O中,AB为直径,∠ACD=45°,已知AC=7,BC=5,则CD =_______
相关试题

