【题目】如图,△ABC中以AB为直径作⊙O,分别交边AC、BC于D、E,过D作DF⊥BC于F,且D为弧AE的中点.
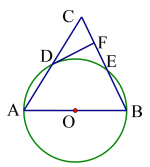
(1)求证:DF为⊙O的切线;
(2)若![]() 且AD=
且AD=![]() 时,求⊙O的半径
时,求⊙O的半径![]() .
.
参考答案:
【答案】(1)见解析;(2)r=10
【解析】
(1)如图,作辅助线;证明AE∥DF;利用垂径定理的推论证明OD⊥AE,即可解决问题.
(2)连接AE交OD于H,根据圆周角的性质求得AE⊥BE,根据垂径定理求得OD⊥AE,从而求得OD∥BC,进而求得OH=![]() BE,根据题意设BE=3x,则AB=5x,由勾股定理得,AE=4x,进而得出AH=2x,OH=1.5x,DH=x,然后根据勾股定理求得AD=
BE,根据题意设BE=3x,则AB=5x,由勾股定理得,AE=4x,进而得出AH=2x,OH=1.5x,DH=x,然后根据勾股定理求得AD=![]() x,又因为AD=4
x,又因为AD=4![]() ,即可求得x=4,进而求得⊙O的半径.
,即可求得x=4,进而求得⊙O的半径.
证明:(1)如图,连接AE、OD;
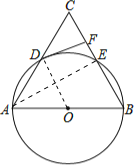
∵AB为⊙O的直径,
∴AE⊥BC,而DF⊥BC,
∴AE∥DF;
∵D为弧AE的中点
∴OD⊥AE,
∴OD⊥DF,
即DF为⊙O的切线.
(2)连接AE交OD于H,
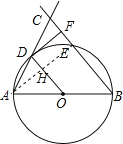
∵AB是⊙O的直径,
∴∠AEB=90°,
即AE⊥BE,
∵D为弧AE的中点,
∴OD⊥AE,
∴OD∥BC,
∵OA=OB,
∴OH=![]() BE,
BE,
在RT△ABE中,![]()
,设BE=3x,则AB=5x,由勾股定理得,AE=4x,
∴AH=2x,OH=1.5x,
∴DH=OD-OH=2.5x-1.5x=x,
在RT△ADH中,AD=![]()
∵AD=4![]() ,
,
∴x=4,
∴⊙O的半径=4×2.5=10.
-
科目: 来源: 题型:
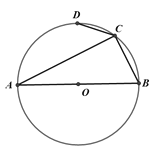
查看答案和解析>>【题目】在⊙O中,AB为直径,∠ACD=45°,已知AC=7,BC=5,则CD =_______
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形
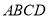 中,
中,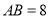 ,
,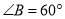 ,
,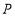 是
是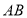 上一点,
上一点,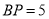 ,
,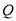 是
是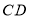 边上一动点,将四边形
边上一动点,将四边形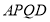 沿直线
沿直线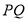 折叠,
折叠,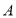 的对应点
的对应点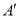 .当
.当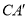 的长度最小时,则
的长度最小时,则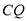 的长为_______
的长为_______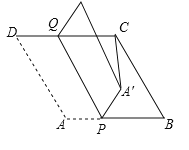
-
科目: 来源: 题型:
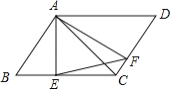
查看答案和解析>>【题目】如图,四边形
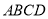 是平行四边形,
是平行四边形,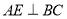 ,
,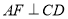 ,垂足分别为
,垂足分别为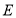 、
、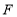 ,连接
,连接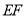 .
.求证:(1)
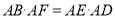 ;(2)
;(2)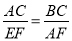 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小区为了改善居住环境,准备修建一个巨型花园ABCD,为了节约材料并种植不同花卉,决定花园一边靠墙,三边用栅栏围住,中间用一段垂直于墙的栅栏隔成两块.已知所用栅栏的总长为60米,墙长为30米,设花园垂直于墙的一边的长为
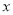 米.
米.
(1)若平行于墙的一边长为
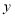 米,直接写出
米,直接写出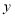 与
与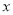 的函数关系式及自变量
的函数关系式及自变量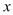 的取值范围;
的取值范围;(2)当
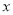 为何值时,这个矩形花园的面积最大?最大值为多少?(栅栏占地面积忽略不计)
为何值时,这个矩形花园的面积最大?最大值为多少?(栅栏占地面积忽略不计)(3)当这个花园的面积不小于288平方米时,试结合函数图象,直接写出
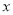 的取值范围
的取值范围 -
科目: 来源: 题型:
查看答案和解析>>【题目】在
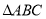 中,
中,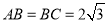 ,
,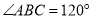 ,
,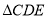 为等边三角形,
为等边三角形,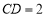 ,连接
,连接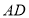 ,
,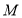 为
为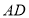 中点.
中点.(1)如图1,当
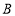 ,
,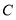 ,
,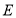 三点共线时,请画出
三点共线时,请画出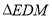 关于点
关于点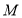 的中心对称图形,判断
的中心对称图形,判断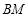 与
与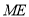 的位置关系是 ;
的位置关系是 ;(2)如图2,当A,
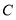 ,
,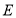 三点共线时,问(1)中结论是否成立,若成立,给出证明,若不成立,请说明理由;
三点共线时,问(1)中结论是否成立,若成立,给出证明,若不成立,请说明理由;(3)如图2,取
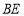 中点
中点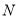 ,连
,连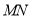 ,将
,将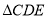 绕点
绕点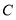 旋转,直接写出旋转过程中线段
旋转,直接写出旋转过程中线段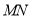 的取值范围是 .
的取值范围是 .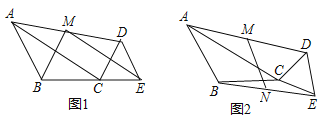
-
科目: 来源: 题型:
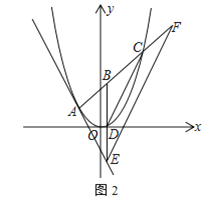
查看答案和解析>>【题目】在平面直角坐标系中,抛物线
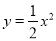 经过点
经过点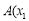 ,
,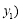 、
、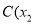 ,
,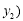 ,其中
,其中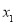 、
、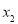 是方程
是方程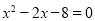 的两根,且
的两根,且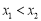 ,过点
,过点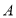 的直线
的直线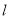 与抛物线只有一个公共点
与抛物线只有一个公共点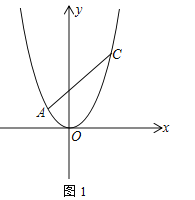
(1)求
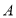 、
、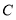 两点的坐标;
两点的坐标;(2)求直线
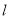 的解析式;
的解析式;(3)如图2,点
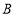 是线段
是线段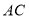 上的动点,若过点
上的动点,若过点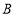 作
作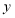 轴的平行线
轴的平行线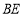 与直线
与直线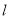 相交于点
相交于点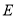 ,与抛物线相交于点
,与抛物线相交于点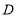 ,过点
,过点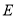 作
作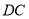 的平行线
的平行线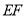 与直线
与直线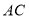 相交于点
相交于点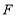 ,求
,求 的长.
的长.
相关试题

