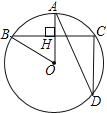
【题目】如图,在⊙O中,半径OA⊥弦BC于点H,点D在优弧BC上
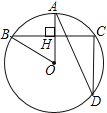
(1)若∠AOB=50°,求∠ADC的度数;
(2)若BC=8,AH=2,求⊙O的半径.
参考答案:
【答案】
【解析】(1)∠ADC=25°;(2)⊙O的半径为5.
试题分析:(1)根据垂径定理可得![]() =
=![]() ,再根据圆周角定理可得∠ADC=
,再根据圆周角定理可得∠ADC=![]() ∠AOB,进而可得答案;
∠AOB,进而可得答案;
(2)根据垂径定理可得BH=4,设HO=x,则AO=BO=x+2,在Rt△BHO中利用勾股定理可得(x+2)2=x2+42,解方程可得x的值,从而可得答案.
解:(1)∵半径OA⊥弦BC于点H,
∴![]() =
=![]() ,
,
∴∠ADC=![]() ∠AOB,
∠AOB,
∵∠AOB=50°,
∴∠ADC=25°;
(2)∵半径OA⊥弦BC于点H,
∴BH=![]() BC,
BC,
∵BC=8,
∴BH=4,
设HO=x,则AO=BO=x+2,
在Rt△BHO中,BO2=HO2+BH2,
∴(x+2)2=x2+42,
解得:x=3,
∴AO=5.
答:⊙O的半径为5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣2×3= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣2﹣(﹣3)=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若2x+1是﹣9的相反数,则x=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数的图象与x轴、y轴分别相交于A、B两点,且与反比例函数y=
 (k≠0)的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.
(k≠0)的图象在第一象限交于点C,如果点B的坐标为(0,2),OA=OB,B是线段AC的中点.
(1)求一次函数解析式及反比例函数的解析式;
(2)若一次函数值大于反比例函数值,请求出相应的自变量x的取值范围.
-
科目: 来源: 题型:
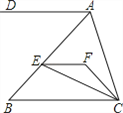
查看答案和解析>>【题目】如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,求∠FEC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,函数y=﹣x+4的图象与坐标轴交于A、B两点,点M(2,m)是直线AB上一点,点N与点M关于y轴对称.

(1)填空:m= ;
(2)点P在平面上,若以A、M、N、P为顶点的四边形是平行四边形,直接写出点P的坐标;
(3)如图2,反比例函数
 的图象经过N、E(x1,y1)、F(x2,y2)三点.且x1>x2,点E、F关于原点对称,若点E到直线MN的距离是点F到直线MN的距离的3倍,求E、F两点的坐标.
的图象经过N、E(x1,y1)、F(x2,y2)三点.且x1>x2,点E、F关于原点对称,若点E到直线MN的距离是点F到直线MN的距离的3倍,求E、F两点的坐标.
相关试题

