【题目】如图,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.

(1)若∠DEC=25°,求∠B的度数;
(2)求证:直线AD是线段CE的垂直平分线.
参考答案:
【答案】(1)∠B=40°;(2)见解析.
【解析】
(1)依据角平分线的的性质,即可得出DE=DC,进而得出∠BDE的度数,再根据DE⊥AB,即可得出∠B的度数;
(2)依据全等三角形的对应边相等,即可得到AE=AC,ED=DC,进而得到点D在CE的垂直平分线上,点A在CE的垂直平分线上.
(1)∵∠ACB=90°,AD平分∠BAC,DE⊥AB,
∴DE=DC,
∴∠DEC=∠DCE=25°,
∴∠BDE=50°,
又∵DE⊥AB,
∴Rt△BDE中,∠B=90°﹣∠BDE=90°﹣50°=40°;
(2)∵DE⊥AB,
∴∠AED=90°=∠ACB,
又∵DE=DC,AD=AD,
∴△AED≌△ACD(HL),
∴ED=DC,AE=AC,
∴点D在CE的垂直平分线上,点A在CE的垂直平分线上,
∴直线AD是线段CE的垂直平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm,点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动,他们的运动时间为t(s).

(1)若点Q的运动速度与点P的运动速度相等,当t=1时,△ACP与△BPQ是否全等,请说明理由
(2)判断此时线段PC和线段PQ的关系,并说明理由。
(3)如图(2),将图(1)中的“AC⊥AB,BD⊥AB”改为“∠CAB=∠DBA=60°”,其他条件不变,设点Q的运动速度为x cm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,求出相应的x、t的值;若不存在,请说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BC为⊙O的直径,点D在⊙O上,连结BD、CD,过点D的切线AE与CB的延长线交于点A,∠BCD=∠AEO,OE与CD交于点F.
(1)求证:OF∥BD;
(2)当⊙O的半径为10,sin∠ADB=
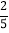 时,求EF的长.
时,求EF的长.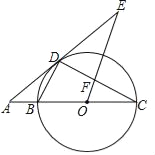
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠BAC=30°,D为角平分线上一点,DE⊥AC于E,DF∥AC,且交AB于点F.

(1)求证:△AFD为等腰三角形;
(2)若DF=10cm,求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】许多数学题目都有多种解法,如题目:如图,已知,∠MAN=120°,AC平分∠MAN.∠ABC+∠ADC=180°.求证:AB+AD=AC.

某班第二学习小组经过讨论,提出了三种添加辅助线的方法,请你选择
其中一种方法,完成证明.
方法一:在AN上截取AE=AC,连接CE:
方法二:过点C作CE∥AM交AN于点E
方法三:过点C分别作CE⊥AN于点E,CF⊥AM于点F.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,AC=BC,∠ACB=90°,CE与AB相交于点D,且BE⊥CE,AF⊥CE,垂足分别为点E、F.
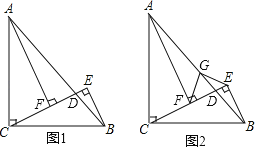
(1)若AF=5,BE=2,求EF的长.
(2)如图2,取AB中点G,连接FC、EC,请判断△GEF的形状,并说明理由.
-
科目: 来源: 题型:
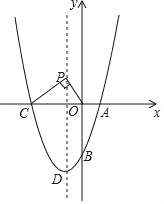
查看答案和解析>>【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、C两点,点A在点C的右边,与y轴交于点B,点B的坐标为(0,﹣3),且OB=OC,点D为该二次函数图象的顶点.
(1)求这个二次函数的解析式及顶点D的坐标;
(2)如图,若点P为该二次函数的对称轴上的一点,连接PC、PO,使得∠CPO=90°,请求出所有符合题意的点P的坐标;
(3)在对称轴上是否存在一点P,使得∠OPC为钝角,若存在,请直接写出点P的纵坐标为yp的取值范围,若没有,请说明理由.
相关试题

