Question

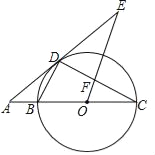
【题目】如图，BC为⊙O的直径，点D在⊙O上，连结BD、CD，过点D的切线AE与CB的延长线交于点A，∠BCD=∠AEO，OE与CD交于点F．

（1）求证：OF∥BD；

（2）当⊙O的半径为10，sin∠ADB=时，求EF的长．

Answer 1

【答案】（1）证明见解析；（2）EF=21．

【解析】

（1）连接OD，如图，利用切线的性质得到OD⊥AE，利用圆周角定理得到∠BDC=90°，然后证明∠ADB=∠AEO得到BD∥OF；

（2）由（1）知，sin∠C=sin∠E=sin∠ADB=．在Rt△BCD中，利用正弦的定义计算出BD=8，再利用三角形中位线性质得到OF=BD=4，接着在Rt△EOD中利用正弦定义计算出OE=25，然后计算OE与OF的差即可．

（1）连接OD，如图，∵AE与O相切，∴OD⊥AE，∴∠ADB+∠ODB=90°．

∵BC为直径，∴∠BDC=90°，即∠ODB+∠ODC=90°，∴∠ADB=∠ODC．

∵OC=OD，∴∠ODC=∠C，而∠BCD=∠AEO，∴∠ADB=∠AEO，∴BD∥OF；

（2）由（1）知，∠ADB=∠E=∠BCD，∴sin∠C=sin∠E=sin∠ADB=．在Rt△BCD中，sin∠C==，∴BD=×20=8．

∵OF∥BD，∴OF=BD=4．在Rt△EOD中，sin∠E==，∴OE=25，∴EF=OE﹣OF=25﹣4=21．