【题目】如图1,在△ABC中,AC=BC,∠ACB=90°,CE与AB相交于点D,且BE⊥CE,AF⊥CE,垂足分别为点E、F.
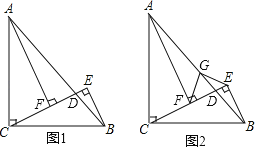
(1)若AF=5,BE=2,求EF的长.
(2)如图2,取AB中点G,连接FC、EC,请判断△GEF的形状,并说明理由.
参考答案:
【答案】(1)EF=3;(2)△GEF为等腰直角三角形;理由见解析.
【解析】
(1)证得∠ACF=∠CBE,由AAS证得△ACF≌△CBE得出CF=BE=2,AF=CE=5,即可得出结果;
(2)连接CG,证得CG⊥AB,∠BCG=![]() ∠ACB=45°,则∠CBG=45°,推出∠GCB=∠CBG=45°,得出CG=BG,易证∠FAD=∠EBG,由△ACF≌△CBE得出CF=BE,∠CAF=∠BCE,证出∠FAD=∠GCD,∠EBG=∠FCG,由SAS证得△CFG≌△BEG得出FG=EG,∠CGF=∠EGB,由∠CGF+∠FGD=90°,得出∠FGD+∠EGB=90°,即∠FGE=90°,即可得出结论.
∠ACB=45°,则∠CBG=45°,推出∠GCB=∠CBG=45°,得出CG=BG,易证∠FAD=∠EBG,由△ACF≌△CBE得出CF=BE,∠CAF=∠BCE,证出∠FAD=∠GCD,∠EBG=∠FCG,由SAS证得△CFG≌△BEG得出FG=EG,∠CGF=∠EGB,由∠CGF+∠FGD=90°,得出∠FGD+∠EGB=90°,即∠FGE=90°,即可得出结论.
(1)∵BE⊥CE,
∴∠BEC=90°,
∵∠ACB=90°,
∴∠BEC=∠ACB,
∴∠ACF+∠BCE=∠BCE+∠CBE=90°,
∴∠ACF=∠CBE,
∵AF⊥CE,
∴∠AFC=90°,
在△ACF和△CBE中,
∵∠ACF=∠CBE,∠AFC=∠BEC,AC=BC,
∴△ACF≌△CBE(AAS),
∴CF=BE=2,AF=CE=5,
∵EF=CE﹣CF,
∴EF=5﹣2=3;
(2)△GEF为等腰直角三角形;理由如下:

连接CG,如图2所示:
∵AC=BC,AG=BG,
∴CG⊥AB,∠BCG=![]() ∠ACB=
∠ACB=![]() ×90°=45°,
×90°=45°,
∴∠CBG=90°﹣45°=45°,
∴∠GCB=∠CBG=45°,
∴CG=BG,
在△ADF和△BDE中,∵∠AFD=∠BED,
∴∠FAD=∠EBG,
由(1)证可知:△ACF≌△CBE,
∴CF=BE,∠CAF=∠BCE,
∵∠CAF+∠FAD=∠GCD+∠BCE=45°,
∴∠FAD=∠GCD,
∴∠EBG=∠FCG,
在△CFG与△BEG中,
∵CG=BG,∠FCG=∠EBG,CF=BE,
∴△CFG≌△BEG(SAS),
∴FG=EG,∠CGF=∠EGB,
∵∠CGF+∠FGD=90°,
∴∠FGD+∠EGB=90°,即∠FGE=90°,
∴△FGE是等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠BAC=30°,D为角平分线上一点,DE⊥AC于E,DF∥AC,且交AB于点F.

(1)求证:△AFD为等腰三角形;
(2)若DF=10cm,求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠ACB=90°,AD平分∠BAC,DE⊥AB于E.

(1)若∠DEC=25°,求∠B的度数;
(2)求证:直线AD是线段CE的垂直平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】许多数学题目都有多种解法,如题目:如图,已知,∠MAN=120°,AC平分∠MAN.∠ABC+∠ADC=180°.求证:AB+AD=AC.

某班第二学习小组经过讨论,提出了三种添加辅助线的方法,请你选择
其中一种方法,完成证明.
方法一:在AN上截取AE=AC,连接CE:
方法二:过点C作CE∥AM交AN于点E
方法三:过点C分别作CE⊥AN于点E,CF⊥AM于点F.
-
科目: 来源: 题型:
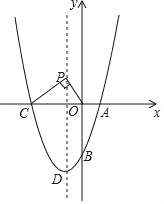
查看答案和解析>>【题目】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、C两点,点A在点C的右边,与y轴交于点B,点B的坐标为(0,﹣3),且OB=OC,点D为该二次函数图象的顶点.
(1)求这个二次函数的解析式及顶点D的坐标;
(2)如图,若点P为该二次函数的对称轴上的一点,连接PC、PO,使得∠CPO=90°,请求出所有符合题意的点P的坐标;
(3)在对称轴上是否存在一点P,使得∠OPC为钝角,若存在,请直接写出点P的纵坐标为yp的取值范围,若没有,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在Rt△ADE中,∠DAE=90°,C是边AE上任意一点(点C与点A、E不重合),以AC为一直角边在Rt△ADE的外部作Rt△ABC,∠BAC=90°,连接BE、CD.
(1)在图1中,若AC=AB,AE=AD,现将图1中的Rt△ADE绕着点A顺时针旋转锐角α,得到图2,那么线段BE.CD之间有怎样的关系,写出结论,并说明理由;
(2)在图1中,若CA=3,AB=5,AE=10,AD=6,将图1中的Rt△ADE绕着点A顺时针旋转锐角α,得到图3,连接BD、CE.
①求证:△ABE∽△ACD;
②计算:BD2+CE2的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.
(1)求证:AD=AG;
(2)AD与AG的位置关系如何,请说明理由.

相关试题

