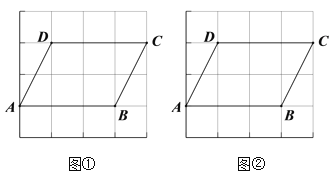
【题目】图①、图②均是4×4的正方形网格,每个小正方形的顶点称为格点,四边形ABCD的顶点均在格点上,仅用无刻度直尺,分别按下列要求画图.
(1)在图①中的线段CD上找到一点E,连结AE,使得AE将四边形ABCD的面积分成1:2两部分.
(2)在图②中的四边形ABCD外部作一条直线l,使得直线l上任意一点与点A、B构成三角形的面积是四边形ABCD面积的![]() .(保留作图痕迹)
.(保留作图痕迹)
参考答案:
【答案】(1)见解析. (2)见解析.
【解析】
(1)利用面积法,数形结合的思想,求出AE解决问题即可.
(2)如图②中,取格点M,N,K,连接MN,MK可得格点T,R,作直线TR,直线TR即为所求.
解:(1)如图,线段AE即为所求.
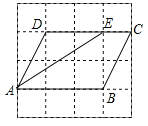
∵S四边形ABCD=3×2=6,S△ADE=![]() ×2×2=2.
×2×2=2.
∴![]() ;
;
(2)如图所示:直线TK为所求;
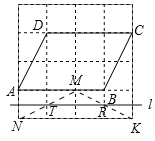
∵S四边形ABCD=3×2=6,
又∵![]() ,
,![]() ,
,
∴![]() ;
;
∴直线l∥AB,并且在AB的下方,距离AB等于![]() 个单位长度.
个单位长度.
-
科目: 来源: 题型:
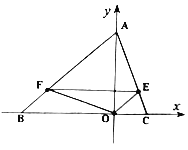
查看答案和解析>>【题目】如图,等腰
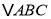 中,
中,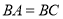 ,
,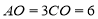 .动点
.动点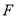 在
在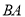 上以每分钟5个单位长度的速度从
上以每分钟5个单位长度的速度从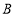 点出发向
点出发向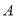 点移动,过
点移动,过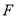 作
作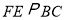 交
交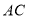 边于
边于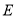 点,连结
点,连结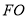 、
、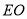 .设
.设 点移动的时间为
点移动的时间为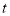 .
.
(1)求
 、
、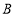 两点的坐标;
两点的坐标;(2)计算:当
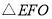 面积最大时,
面积最大时,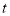 的值;
的值;(3)在(2)的条件下,边
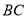 上是否还存在一个点
上是否还存在一个点 ,使得
,使得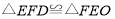 ?若存在,请直接写出
?若存在,请直接写出 点的坐标;若不存在,试说明理由.
点的坐标;若不存在,试说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①,四边形 ABCD 是正方形,点 G 是 BC 上的任意一点,BF AG 于点 F,DE AG于点 E,探究 BF,DE,EF 之间的数量关系.第一学习小组合作探究后,得到DE–BF= EF,请证明这个结论;
(2)若(1)中的点 G 在 CB 的延长线上,其余条件不变,请在图②中画出图形,并直接写出此时 BF,DE,EF 之间的数量关系;
(3)如图 ③ ,四边形 ABCD 内接于 ⊙O,AB=AD,E ,F 是AC 上的两点,且满足∠AED=∠BFA=∠BCD.试判断 AC,DE,BF 之间的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数
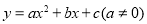 的图象交
的图象交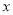 轴于
轴于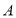 、
、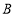 两点,交
两点,交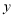 轴于点
轴于点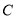 ,点
,点 为该二次函数图象顶点.连接
为该二次函数图象顶点.连接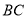 、
、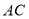 及
及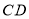 、
、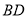 .
.

(1)如图1,若点
 的坐标
的坐标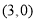 ,顶点
,顶点 坐标
坐标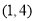 .
.①求
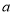 的值,并说明
的值,并说明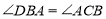 ;
;②如图2,点
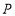 是抛物线的对称轴上一点,以点
是抛物线的对称轴上一点,以点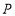 为圆心的圆经过
为圆心的圆经过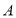 、
、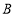 两点,且与直线
两点,且与直线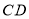 相切,求点
相切,求点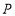 的坐标;
的坐标;(2)若
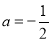 ,点
,点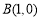 ,点
,点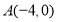 ,如图3,动点
,如图3,动点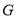 在直线
在直线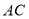 上方的二次函数图象上.过点
上方的二次函数图象上.过点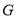 作
作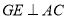 于点
于点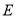 ,是否存在点
,是否存在点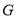 ,使得
,使得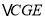 中的某个角恰好等于
中的某个角恰好等于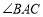 的2倍?若存在,求出点
的2倍?若存在,求出点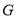 的横坐标:若不存在,请说明理由.
的横坐标:若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】根据以下信息,解答下列问题.

(1)小华同学设乙型机器人每小时搬运xkg产品,可列方程为 .
小惠同学设甲型机器人搬运800kg所用时间为y小时,可列方程为 .
(2)请你按照(1)中小华同学的解题思路,写出完整的解答过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校开展“江山如此多娇”为主题的地理知识竞赛活动,要求每班派出一名同学代表本班参赛.九年一班四名同学主动报名,老师为了确定最终参赛人选,对这四名同学的历次地理考试成绩进行了汇总,数据如下:

班级里数学小组的同学对上面的数据进行了进一步的整理:

根据以上的信息,回答下列问题:
(1)写出上表中
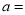 ,
, ,
,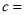 .
.(2)丙同学看到统计表,对老师说:“我的成绩方差最小,说明我的成绩最稳定,应该派我去参赛!”请问你是否同意他的观点?若你是老师,你将派谁参赛?说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一条河流经过
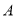 、
、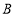 两个港口,水流的速度是4千米/时.甲、乙两船同时出发,由
两个港口,水流的速度是4千米/时.甲、乙两船同时出发,由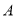 港口顺流驶向
港口顺流驶向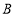 港口,甲船的静水速度快于乙船的静水速度.两船分别到达
港口,甲船的静水速度快于乙船的静水速度.两船分别到达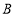 港口后立即返回
港口后立即返回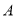 港口.两船与
港口.两船与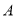 港口的距离
港口的距离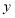 (千米)与出发时间
(千米)与出发时间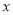 (时)之间的函数图像如图所示.
(时)之间的函数图像如图所示.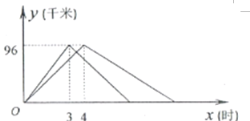
(1)
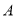 、
、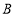 两港口相距 千米.乙船在静水中的速度为 千米/时.
两港口相距 千米.乙船在静水中的速度为 千米/时.(2)求甲船从
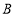 港口返回
港口返回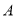 港口时
港口时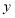 与
与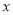 之间的函数关系式.
之间的函数关系式.(3)求两船在途中相遇时,相遇处于
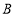 港口之间的距离.
港口之间的距离.
相关试题

