【题目】一条河流经过![]() 、
、![]() 两个港口,水流的速度是4千米/时.甲、乙两船同时出发,由
两个港口,水流的速度是4千米/时.甲、乙两船同时出发,由![]() 港口顺流驶向
港口顺流驶向![]() 港口,甲船的静水速度快于乙船的静水速度.两船分别到达
港口,甲船的静水速度快于乙船的静水速度.两船分别到达![]() 港口后立即返回
港口后立即返回![]() 港口.两船与
港口.两船与![]() 港口的距离
港口的距离![]() (千米)与出发时间
(千米)与出发时间![]() (时)之间的函数图像如图所示.
(时)之间的函数图像如图所示.
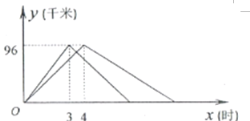
(1)![]() 、
、![]() 两港口相距 千米.乙船在静水中的速度为 千米/时.
两港口相距 千米.乙船在静水中的速度为 千米/时.
(2)求甲船从![]() 港口返回
港口返回![]() 港口时
港口时![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(3)求两船在途中相遇时,相遇处于![]() 港口之间的距离.
港口之间的距离.
参考答案:
【答案】(1)96,20;(2)![]() ;(3)12千米
;(3)12千米
【解析】
(1)根据图象即可得出A、B两港口相距96千米;根据乙船由A港口顺流驶向B港口用了4小时列出方程即可求得乙船在静水中的速度;
(2)根据甲船向A港口顺流驶向B港口时3小时可得出甲船逆水速度,进而得出甲船从B港口返回A港口时y与x之间的函数关系式;
(3)根据(2)的结论以及乙船由A港口顺流驶向B港口时y与x之间的函数关系式列方程即可解答.
解:(1)由图象可知,A、B两港口相距96千米,
设乙船在静水中的速度为x千米/时
4×(x+4)=96,
解得x=20,
即乙船在静水中的速度为20千米/时,
(2)甲船在顺水的速度为:![]() (千米/时),
(千米/时),
∴甲船逆水速度为:32-8=24(千米/时),
∴![]() .
.
即甲船从B港口返回A港口时y与x之间的函数关系式为:![]() .
.
(3)根据题意得:![]() ,
,
解得![]() ,
,![]() .
.
![]() 两船在途中相遇时,相遇处于
两船在途中相遇时,相遇处于![]() 港口相距12千米.
港口相距12千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】图①、图②均是4×4的正方形网格,每个小正方形的顶点称为格点,四边形ABCD的顶点均在格点上,仅用无刻度直尺,分别按下列要求画图.
(1)在图①中的线段CD上找到一点E,连结AE,使得AE将四边形ABCD的面积分成1:2两部分.
(2)在图②中的四边形ABCD外部作一条直线l,使得直线l上任意一点与点A、B构成三角形的面积是四边形ABCD面积的
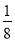 .(保留作图痕迹)
.(保留作图痕迹)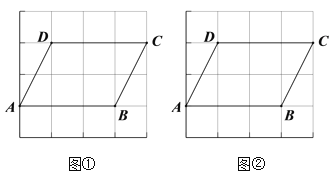
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据以下信息,解答下列问题.

(1)小华同学设乙型机器人每小时搬运xkg产品,可列方程为 .
小惠同学设甲型机器人搬运800kg所用时间为y小时,可列方程为 .
(2)请你按照(1)中小华同学的解题思路,写出完整的解答过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校开展“江山如此多娇”为主题的地理知识竞赛活动,要求每班派出一名同学代表本班参赛.九年一班四名同学主动报名,老师为了确定最终参赛人选,对这四名同学的历次地理考试成绩进行了汇总,数据如下:

班级里数学小组的同学对上面的数据进行了进一步的整理:

根据以上的信息,回答下列问题:
(1)写出上表中
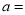 ,
, ,
,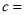 .
.(2)丙同学看到统计表,对老师说:“我的成绩方差最小,说明我的成绩最稳定,应该派我去参赛!”请问你是否同意他的观点?若你是老师,你将派谁参赛?说明你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(感知)如图①,正方形
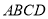 中,点
中,点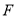 在
在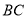 边上,
边上,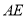 平分
平分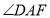 .若我们分别延长
.若我们分别延长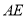 与
与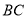 ,交于点
,交于点 ,则易证
,则易证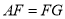 .(不需要证明)
.(不需要证明)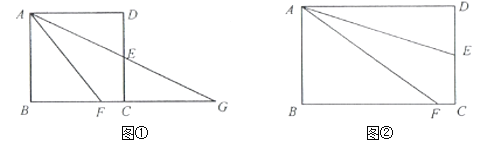
(探究)如图②,在矩形
 中,点
中,点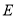 在
在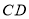 边的中点,点
边的中点,点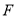 在
在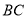 边上,
边上,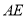 平分
平分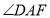 .求证:
.求证: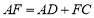 .
.(应用)在(探究)的条件下,若
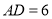 ,
,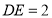 ,直接写出
,直接写出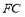 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在等边
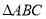 中,
中,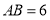 ,动点
,动点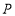 从点
从点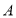 出发,沿
出发,沿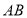 边以每秒1个单位的速度向终点
边以每秒1个单位的速度向终点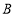 运动,同时动点
运动,同时动点 从点
从点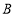 出发,以每秒2个单位的速度沿着
出发,以每秒2个单位的速度沿着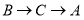 方向运动.连结
方向运动.连结 ,设点
,设点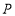 运动的时间
运动的时间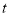 秒.
秒.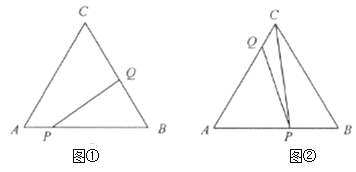
(1)用含
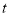 的代数式表示线段
的代数式表示线段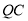 的长.
的长.(2)当
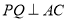 时,求
时,求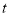 的值.
的值.(3)若
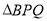 的面积为
的面积为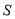 ,求
,求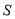 与
与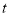 之间的函数关系式.
之间的函数关系式.(4)如图②,当点
 在
在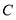 、
、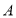 之间时,连结
之间时,连结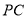 ,
,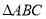 被分割成
被分割成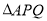 、
、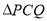 、
、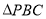 ,当其中的某两个三角形面积相等时,直接写出
,当其中的某两个三角形面积相等时,直接写出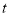 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点
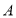 坐标为
坐标为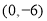 ,点
,点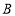 在
在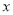 轴的负半轴上,点
轴的负半轴上,点 、
、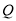 均在线段
均在线段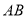 上,且
上,且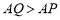 ,点
,点 的横坐标为
的横坐标为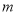 .在
.在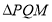 中,若
中,若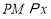 轴,
轴,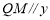 轴,则称
轴,则称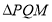 为点
为点 、
、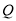 的“榕树三角形”.
的“榕树三角形”.(1)若点
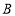 坐标为
坐标为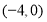 ,且
,且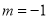 ,则点
,则点 、
、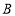 的“榕树三角形”的面积为 .
的“榕树三角形”的面积为 .(2)当点
 、
、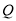 的“榕树三角形”是等腰三角形时,求点
的“榕树三角形”是等腰三角形时,求点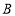 的坐标.
的坐标.(3)在(2)的条件下,作过
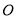 、
、 、
、 三点的抛物线
三点的抛物线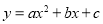 .
.①若
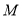 点必为抛物线上一点,求点
点必为抛物线上一点,求点 、
、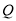 的“榕树三角形”面积
的“榕树三角形”面积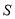 与
与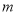 之间的函数关系式.
之间的函数关系式.②当点
 、
、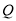 的“榕树三角形”面积2,且抛物线
的“榕树三角形”面积2,且抛物线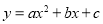 与点
与点 、
、 的“榕树三角形”恰有两个交点时,直接写出
的“榕树三角形”恰有两个交点时,直接写出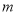 的取值范围.
的取值范围.
相关试题

