【题目】(1)如图①,四边形 ABCD 是正方形,点 G 是 BC 上的任意一点,BF AG 于点 F,DE AG于点 E,探究 BF,DE,EF 之间的数量关系.第一学习小组合作探究后,得到DE–BF= EF,请证明这个结论;
(2)若(1)中的点 G 在 CB 的延长线上,其余条件不变,请在图②中画出图形,并直接写出此时 BF,DE,EF 之间的数量关系;
(3)如图 ③ ,四边形 ABCD 内接于 ⊙O,AB=AD,E ,F 是AC 上的两点,且满足∠AED=∠BFA=∠BCD.试判断 AC,DE,BF 之间的数量关系,并说明理由.

参考答案:
【答案】(1)证明见解析;(2)EF=BF+DE;(3)AC=BF+DE,证明见解析
【解析】(1)∵正方形ABCD,BF⊥AG,DE⊥AG
∴ AB=AD,
∠BAF+∠DAE=∠BAF+∠ABF=∠AFB=∠DEA=900
∴∠DAE=∠ABF
∴△ADE≌△BAF
∴BF=AE,AF=DE
∴ EF= AF –AE = DE– BF

(2)作图如图所示

EF=BF+DE
(3)∵ 四边形ABCD内接于圆
∴ ∠BCD+∠BAD=1800
∵ ∠AED=∠BCD,∠AED+∠DEC=1800
∴∠BAD=∠DEC
∵ ∠BAD=∠1+∠2,∠DEC=∠1+∠3
∴∠2=∠3
∵∠AED=∠BFA,AB=AD
∴ △ADE≌△BAF
∴ AE=BF,DE=AF
连接BD
∵∠AED=∠BCD,∠1=∠DBC
∴∠3=∠4
∴∠ADB=∠EDC
∵AB=AD
∴∠ADB=∠ABD=∠ACD
∴ ∠EDC=∠ACD
∴ DE=CE=AF
∴ AC=AE+CE=BF+DE

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列一元二次方程中,没有实数根的是( )
A. x2=4 B. x(x﹣1)=0 C. x2+x﹣1=0 D. x2+x+1=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校实施课程改革,为初三学生设置了 A,B,C,D,E,F 共六门不同的拓展性课程,现随机抽取若干学生进行了“我最想选的一门课”调查,并将调查结果绘制成如图统计图表(不完整)根据图表提供的信息,下列结论错误的是( )


A. 这次被调查的学生人数为200人
B. 扇形统计图中E部分扇形的圆心角为72°
C. 被调查的学生中最想选 F 的人数为 35 人
D. 被调查的学生中最想选 D 的有 55 人
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)2x+5=5x-7 (2)3(x-2)=2-5(x-2)
(3)
 (4) y-
(4) y- (y-1)=
(y-1)=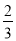 (y-1)
(y-1) -
科目: 来源: 题型:
查看答案和解析>>【题目】下列条件中不可以判定两个直角三角形全等的是( )
A. 两条直角边对应相等 B. 斜边和直角边对应相等
C. 一条边和一锐角对应相等 D. 两个角对应相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市居民生活用电基本价格为每千瓦时0.60元,若每月用电量超过70千瓦时,超出部分按照基本电价的120%收费.
(1)若小明家用电量用a表示,请用代数式分别表示出用电量不超过70千瓦时和超过70千瓦时的收费标准.
(2)若该户居民8月份用电量为100千瓦时,则应收费多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】一个三角形的三边长为5,y,13,若另一个和它全等的三角形三边长为5,12,x,则x+y=______.
相关试题

