【题目】如图,二次函数![]() 的图象交
的图象交![]() 轴于
轴于![]() 、
、![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,点
,点![]() 为该二次函数图象顶点.连接
为该二次函数图象顶点.连接![]() 、
、![]() 及
及![]() 、
、![]() .
.

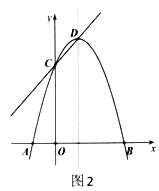

(1)如图1,若点![]() 的坐标
的坐标![]() ,顶点
,顶点![]() 坐标
坐标![]() .
.
①求![]() 的值,并说明
的值,并说明![]() ;
;
②如图2,点![]() 是抛物线的对称轴上一点,以点
是抛物线的对称轴上一点,以点![]() 为圆心的圆经过
为圆心的圆经过![]() 、
、![]() 两点,且与直线
两点,且与直线![]() 相切,求点
相切,求点![]() 的坐标;
的坐标;
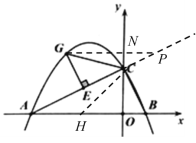
(2)若![]() ,点
,点![]() ,点
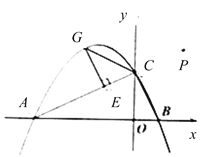
,点![]() ,如图3,动点
,如图3,动点![]() 在直线
在直线![]() 上方的二次函数图象上.过点
上方的二次函数图象上.过点![]() 作
作![]() 于点
于点![]() ,是否存在点
,是否存在点![]() ,使得
,使得![]() 中的某个角恰好等于
中的某个角恰好等于![]() 的2倍?若存在,求出点
的2倍?若存在,求出点![]() 的横坐标:若不存在,请说明理由.
的横坐标:若不存在,请说明理由.
参考答案:
【答案】(1)①![]() ,见解析;②点P的坐标为(1,﹣4+
,见解析;②点P的坐标为(1,﹣4+![]() )或(1,﹣4﹣
)或(1,﹣4﹣![]() );(2)G的横坐标
);(2)G的横坐标![]() 或
或![]()
【解析】
(1)①设![]() ,将点B坐标代入,求出a值,得到抛物线表达式,令y=0,求出点A坐标,根据OB和OC得出∠CBO=∠OCB,再根据各点坐标算出BC,DC,BD的长,证明△BCD是直角三角形,推出∠DBC=∠OCA,从而得到结论;
,将点B坐标代入,求出a值,得到抛物线表达式,令y=0,求出点A坐标,根据OB和OC得出∠CBO=∠OCB,再根据各点坐标算出BC,DC,BD的长,证明△BCD是直角三角形,推出∠DBC=∠OCA,从而得到结论;
②设直线CD切⊙P于点E.连结PE、PA,作CF⊥DQ于点F,证明△DEP为等腰三角形,设P(1,m),在△APQ中,利用勾股定理列出方程,解出m,可得点P坐标;
(2)分![]() ,
,![]() 两种情况分别讨论,列出相应方程,解之即可.
两种情况分别讨论,列出相应方程,解之即可.
解:(1)①设![]() ,将B(3,0)代入,
,将B(3,0)代入,
解得![]() ,
,
∴抛物线的解析式是:![]() ,即
,即![]() ,
,
令![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,
∴A(-1,0),
∴![]() ,
,
∴∠CBO=∠OCB,![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() 是直角三角形且
是直角三角形且![]() ,
,
∴![]() ,
,
又∵∠DBC和∠OCA都是锐角,
∴∠DBC=∠OCA,
∴∠DBA=∠ACB;
②如图,设直线CD切⊙P于点E.连结PE、PA,作CF⊥DQ于点F,
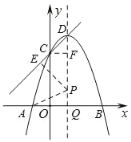
∴PE⊥CD,PE=PA,
由y=﹣x2+2x+3,得:对称轴为直线x=1,C(0,3)、D(1,4),
∴DF=4﹣3=1,CF=1,
∴DF=CF,
∴△DCF为等腰直角三角形,
∴∠CDF=45°,
∴∠EDP=∠EPD=45°,
∴DE=EP,
∴△DEP为等腰三角形,
设P(1,m),D(1,4),
∴![]() ,
,
∴![]() ,
,
∴EP2=![]() (4﹣m)2,
(4﹣m)2,
在△APQ中,∠PQA=90°,
∴AP2=AQ2+PQ2=[1-(-1)]2+m2
∴![]() (4﹣m)2=[1-(-1)]2+m2,
(4﹣m)2=[1-(-1)]2+m2,
整理,得m2+8m﹣8=0,
解得,m=﹣4±![]() ,
,
∴点P的坐标为(1,﹣4+![]() )或(1,﹣4﹣
)或(1,﹣4﹣![]() );
);
(2)G的横坐标![]() 或
或![]() ,
,
①若![]() ,
,
∴![]() ,
,
∴![]() ,
,
当![]() 时,
时,
![]() ,
,
∴![]() ,
,
于是,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() (舍),
(舍),![]() ,
,
∴![]() ;
;
②若![]() ,
,
取![]() 的中点
的中点![]() ,
,
则![]() ,
,
∴![]() ,
,
∴![]() ,
,
令![]() ,
,![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴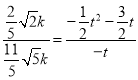 ,
,
∴![]() ,
,
∴![]()
故点G的横坐标![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】受国内外复杂多变的经济环境影响,去年1至7月,原材料价格一路攀升,长沙市某服装厂每件衣服原材料的成本y1(元)与月份x(1≤x≤7,且x为整数)之间的函数关系如下表:
月份x
1
2
3
4
5
6
7
成本(元/件)
56
58
60
62
64
66
68
8至12月,随着经济环境的好转,原材料价格的涨势趋缓,每件原材料成本y2(元)与月份x的函数关系式为y2=x+62(8≤x≤12,且x为整数).
(1)请观察表格中的数据,用学过的函数相关知识求y1与x的函数关系式.
(2)若去年该衣服每件的出厂价为100元,生产每件衣服的其他成本为8元,该衣服在1至7月的销售量p1(万件)与月份x满足关系式p1=0.1x+1.1(1≤x≤7,且x为整数); 8至12月的销售量p2(万件)与月份x满足关系式p2=﹣0.1x+3(8≤x≤12,且x为整数),该厂去年哪个月利润最大;并求出最大利润.
-
科目: 来源: 题型:
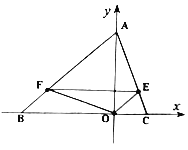
查看答案和解析>>【题目】如图,等腰
 中,
中,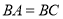 ,
,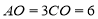 .动点
.动点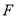 在
在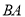 上以每分钟5个单位长度的速度从
上以每分钟5个单位长度的速度从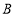 点出发向
点出发向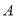 点移动,过
点移动,过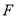 作
作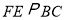 交
交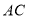 边于
边于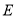 点,连结
点,连结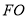 、
、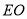 .设
.设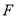 点移动的时间为
点移动的时间为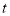 .
.
(1)求
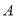 、
、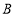 两点的坐标;
两点的坐标;(2)计算:当
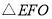 面积最大时,
面积最大时,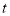 的值;
的值;(3)在(2)的条件下,边
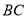 上是否还存在一个点
上是否还存在一个点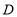 ,使得
,使得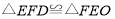 ?若存在,请直接写出
?若存在,请直接写出 点的坐标;若不存在,试说明理由.
点的坐标;若不存在,试说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①,四边形 ABCD 是正方形,点 G 是 BC 上的任意一点,BF AG 于点 F,DE AG于点 E,探究 BF,DE,EF 之间的数量关系.第一学习小组合作探究后,得到DE–BF= EF,请证明这个结论;
(2)若(1)中的点 G 在 CB 的延长线上,其余条件不变,请在图②中画出图形,并直接写出此时 BF,DE,EF 之间的数量关系;
(3)如图 ③ ,四边形 ABCD 内接于 ⊙O,AB=AD,E ,F 是AC 上的两点,且满足∠AED=∠BFA=∠BCD.试判断 AC,DE,BF 之间的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】图①、图②均是4×4的正方形网格,每个小正方形的顶点称为格点,四边形ABCD的顶点均在格点上,仅用无刻度直尺,分别按下列要求画图.
(1)在图①中的线段CD上找到一点E,连结AE,使得AE将四边形ABCD的面积分成1:2两部分.
(2)在图②中的四边形ABCD外部作一条直线l,使得直线l上任意一点与点A、B构成三角形的面积是四边形ABCD面积的
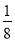 .(保留作图痕迹)
.(保留作图痕迹)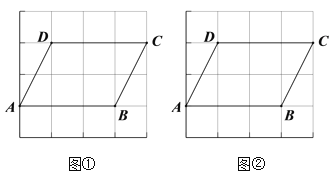
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据以下信息,解答下列问题.

(1)小华同学设乙型机器人每小时搬运xkg产品,可列方程为 .
小惠同学设甲型机器人搬运800kg所用时间为y小时,可列方程为 .
(2)请你按照(1)中小华同学的解题思路,写出完整的解答过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校开展“江山如此多娇”为主题的地理知识竞赛活动,要求每班派出一名同学代表本班参赛.九年一班四名同学主动报名,老师为了确定最终参赛人选,对这四名同学的历次地理考试成绩进行了汇总,数据如下:

班级里数学小组的同学对上面的数据进行了进一步的整理:

根据以上的信息,回答下列问题:
(1)写出上表中
 ,
, ,
, .
.(2)丙同学看到统计表,对老师说:“我的成绩方差最小,说明我的成绩最稳定,应该派我去参赛!”请问你是否同意他的观点?若你是老师,你将派谁参赛?说明你的理由.
相关试题

