搜索
【题目】某超市为了吸引顾客，设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球，球上分别标有“0元”、"10元”、“20元”、“30元”的字样.规定:顾客在本超市一次性消费满200元，就可以在箱子里先后摸出两个小球(每一次摸出后不放回).某顾客刚好消费200元，则该顾客所获得购物券的金额不低于30元的概率.
参考答案：
【答案】
【解析】列表：
第二次第一次 | 0 | 10 | 20 | 30 |
0 | -- | 10 | 20 | 30 |
10 | 10 | -- | 30 | 40 |
20 | 20 | 30 | -- | 50 |
30 | 30 | 40 | 50 | -- |
从上表可以看出，共有12种可能结果，其中大于或等于30元共有8种可能结果，因此P（不低于30元）= 
．
根据列表得到共有12种可能结果，其中大于或等于30元共有8种可能结果，求出该顾客所获得购物券的金额不低于30元的概率.
-
科目： 来源： 题型：
查看答案和解析>>【题目】抛物线
的顶点为 
，与 
轴的一个交点 
在点(-3, 0)和(-2 ,0)之间，其部分图象如图，则以下结论:① 
<0 ;② 
<0;③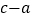 
=2;④方程 
有两个相等的实数根，其中正确结论的个数为个.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，点A、C分别在x轴上、y轴上，CB//OA，OA=8，若点B的坐标为(a,b)，且b=
.（1）直接写出点A、B、C的坐标；
（2）若动点P从原点O出发沿x轴以每秒2个单位长度的速度向右运动，当直线PC把四边形OABC分成面积相等的两部分停止运动，求P点运动时间；
（3）在（2）的条件下，在y轴上是否存在一点Q，连接PQ，使三角形CPQ的面积与四边形OABC的面积相等？若存在，求点Q的坐标；若不存在，请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】早上，小明从家里步行去学校，出发一段时间后，小明妈妈发现小明的作业本落在家里，便带上作业本骑车追赶，途中追上小明两人稍作停留，妈妈骑车返回，小明继续步行前往学校，两人同时到达．设小明在途的时间为x，两人之间的距离为y，则下列选项中的图象能大致反映y与x之间关系的是（ ）
A.
B. 
C.
D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，二次函数y=ax2-6ax+4a+3的图像与y轴交于点A，点B是x轴上一点，其坐标为(1，0)，连接AB,tan∠ABO=2.
（1）则点A的坐标为 ， a=;
（2）过点A作AB的垂线与该二次函数的图像交于另一点C，求点C的坐标;
（3）连接BC，过点A作直线l交线段BC于点P，设点B、点C到l的距离分别为d1、d2 ， 求d1+d2的最大值. -
科目： 来源： 题型：
查看答案和解析>>【题目】为了响应“足球进校园”的号召，学校开设了足球兴趣拓展班，计划同时购买A，B两种足球30个，A，B两种足球的价格分别为50元
个，80元个，设购买B种足球x个，购买两种足球的总费用为y元．
求y关于x的函数表达式．
在总费用不超过1600元的前提下，从节省费用的角度来考虑，求总费用的最小值．
因足球兴趣拓展班的人数增多，所以实际购买中这两种足球总数超过30个，总费用为2000元，则该学校可能共购买足球______个
直接写出答案
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，
是⊙ 
的直径， 
、 
为⊙ 上位于 异侧的两点，连接 
并延长至点 
，使得 
，连接 
交⊙ 于点 
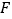，连接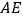 
、 
、 
.
（1）证明:
;
（2）若
，求 
的度数;
（3）设 交 于点 
，若 
是 
的中点，求 
的值.
相关试题
