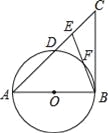
【题目】如图,在△ABC中,E是AC边上的一点,且AE=AB,∠BAC=2∠CBE,以AB为直径作⊙O交AC于点D,交BE于点F.
(1)求证:BC是⊙O的切线;
(2)若AB=8,BC=6,求DE的长.
参考答案:
【答案】(1)证明过程见解析;(2)1.6
【解析】试题分析:(1)由AE=AB,可得∠ABE=90°﹣![]() ∠BAC,又由∠BAC=2∠CBE,可求得∠ABC=∠ABE+∠CBE=90°,继而证得结论;
∠BAC,又由∠BAC=2∠CBE,可求得∠ABC=∠ABE+∠CBE=90°,继而证得结论;
(2)首先连接BD,易证得△ABD∽△ACB,然后由相似三角形的对应边成比例,求得答案.
试题解析:(1)∵AE=AB,
∴△ABE是等腰三角形,
∴∠ABE=![]() (180°﹣∠BAC=)=90°﹣
(180°﹣∠BAC=)=90°﹣![]() ∠BAC,
∠BAC,
∵∠BAC=2∠CBE,
∴∠CBE=![]() ∠BAC,
∠BAC,
∴∠ABC=∠ABE+∠CBE=(90°﹣![]() ∠BAC)+
∠BAC)+![]() ∠BAC=90°,
∠BAC=90°,
即AB⊥BC,
∴BC是⊙O的切线;
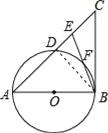
(2)连接BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠ABC=90°,
∴∠ADB=∠ABC,
∵∠A=∠A,
∴△ABD∽△ACB,
∴![]() ,
,
∵在Rt△ABC中,AB=8,BC=6,
∴AC=![]() =10,
=10,
∴![]() ,
,
解得:AD=6.4,
∵AE=AB=8,
∴DE=AE﹣AD=8﹣6.4=1.6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程(m+3)x2+5x+m2-9=0有一个解是0,则m的值为( )
A. -3 B. 3 C. ±3 D. 不确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:3x2y(﹣2xy)结果是( )
A.6x3y2
B.﹣6x3y2
C.﹣6x2y
D.﹣6x2y2 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是假命题的是( )
A. 对角线互相垂直且相等的平行四边形是正方形
B. 对角线互相垂直的矩形是正方形
C. 对角线相等的菱形是正方形
D. 对角线互相垂直的四边形是正方形
-
科目: 来源: 题型:
查看答案和解析>>【题目】将半圆绕直径旋转一周,形成的几何体是________;将直角三角形以一条直角边为轴旋转一周,形成的几何体是________;假如我们把笔尖看作一个点,当笔尖在纸上移动时,就能画出线,说明了________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:已知点P(x0,y0)和直线y=kx+b,则点P到直线y=kx+b的距离,可用公式d=
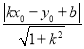 计算.
计算.例如:求点P(﹣1,2)到直线y=3x+7的距离.
解:因为直线y=3x+7,其中k=3,b=7.
所以点P(﹣1,2)到直线y=3x+7的距离为:d=
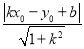 =
=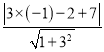 =
=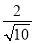 =
=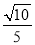 .
.根据以上材料,解答下列问题:
(1)求点P(1,﹣1)到直线y=x﹣1的距离;
(2)已知⊙Q的圆心Q坐标为(0,5),半径r为2,判断⊙Q与直线y=
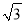 x+9的位置关系并说明理由;
x+9的位置关系并说明理由;(3)已知直线y=﹣2x+4与y=﹣2x﹣6平行,求这两条直线之间的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上与原点的距离不大于4的整数的点有_____个,它们分别是_____.
相关试题

