【题目】阅读理解:已知点P(x0,y0)和直线y=kx+b,则点P到直线y=kx+b的距离,可用公式d=![]() 计算.
计算.
例如:求点P(﹣1,2)到直线y=3x+7的距离.
解:因为直线y=3x+7,其中k=3,b=7.
所以点P(﹣1,2)到直线y=3x+7的距离为:d=![]() =
=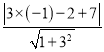 =
=![]() =
=![]() .
.
根据以上材料,解答下列问题:
(1)求点P(1,﹣1)到直线y=x﹣1的距离;
(2)已知⊙Q的圆心Q坐标为(0,5),半径r为2,判断⊙Q与直线y=![]() x+9的位置关系并说明理由;
x+9的位置关系并说明理由;
(3)已知直线y=﹣2x+4与y=﹣2x﹣6平行,求这两条直线之间的距离.
参考答案:
【答案】(1)点P(1,﹣1)到直线y=x﹣1的距离为:d=![]() ;
;
(2)⊙Q与直线y=![]() x+9的位置关系为相切,理由见解析;
x+9的位置关系为相切,理由见解析;
(3)这两条直线之间的距离为2![]()
【解析】解:(1)因为直线y=x﹣1,其中k=1,b=﹣1,
所以点P(1,﹣1)到直线y=x﹣1的距离为:d=![]() =
=![]() =
=![]() =
=![]() ;(3分)
;(3分)
(2)⊙Q与直线y=![]() x+9的位置关系为相切.
x+9的位置关系为相切.
理由如下:圆心Q(0,5)到直线y=![]() x+9的距离为:d=
x+9的距离为:d=![]() =
=![]() =2,
=2,
而⊙O的半径r为2,即d=r,所以⊙Q与直线y=![]() x+9相切;(3分)
x+9相切;(3分)
(3)当x=0时,y=﹣2x+4=4,即点(0,4)在直线y=﹣2x+4,
因为点(0,4)到直线y=﹣2x﹣6的距离为:d=![]() =
=![]() =2
=2![]() ,
,
因为直线y=﹣2x+4与y=﹣2x﹣6平行,所以这两条直线之间的距离为2![]() .(10分)
.(10分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是假命题的是( )
A. 对角线互相垂直且相等的平行四边形是正方形
B. 对角线互相垂直的矩形是正方形
C. 对角线相等的菱形是正方形
D. 对角线互相垂直的四边形是正方形
-
科目: 来源: 题型:
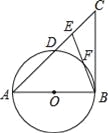
查看答案和解析>>【题目】如图,在△ABC中,E是AC边上的一点,且AE=AB,∠BAC=2∠CBE,以AB为直径作⊙O交AC于点D,交BE于点F.
(1)求证:BC是⊙O的切线;
(2)若AB=8,BC=6,求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将半圆绕直径旋转一周,形成的几何体是________;将直角三角形以一条直角边为轴旋转一周,形成的几何体是________;假如我们把笔尖看作一个点,当笔尖在纸上移动时,就能画出线,说明了________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上与原点的距离不大于4的整数的点有_____个,它们分别是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=3x-5的图像不经过第_____________象限.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是某市一座人行天桥的示意图,天桥离地面的高BC是10米,坡面10米处有一建筑物HQ,为了方便使行人推车过天桥,市政府部门决定降低坡度,使新坡面DC的倾斜角∠BDC=30°,若新坡面下D处与建筑物之间需留下至少3米宽的人行道,问该建筑物是否需要拆除(计算最后结果保留一位小数).(参考数据:
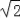 =1.414,
=1.414, =1.732)
=1.732)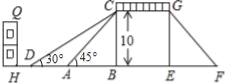
相关试题

