【题目】阅读下列材料:
小明在一本课外读物上看到一道有意思的数学题:例1、解不等式:![]() ,根据绝对值的几何意义,到原点距离小于1的点在数轴上集中在-1和+1之间,如图:
,根据绝对值的几何意义,到原点距离小于1的点在数轴上集中在-1和+1之间,如图:
![]()
所以,该不等式的解集为-1<x<1.
因此,不等式![]() 的解集为x<-1或x>1.
的解集为x<-1或x>1.
根据以上方法小明继续探究:例2:求不等式:![]() 的解集,即求到原点的距离大于2小于5的点的集合就集中在这样的区域内,如图:
的解集,即求到原点的距离大于2小于5的点的集合就集中在这样的区域内,如图:
![]()
所以,不等式![]() 的解集为-5<x<-2或2<x<5.
的解集为-5<x<-2或2<x<5.
仿照小明的做法解决下面问题:
(1)不等式![]() 的解集为____________.
的解集为____________.
(2)不等式![]() 的解集是____________.
的解集是____________.
(3)求不等式![]() 的解集.
的解集.
参考答案:
【答案】(1)-5<x<5 ;(2)-3<x<-1或1<x<3;(3)0<x<4.
【解析】
(1)参照范例1解答即可;
(2)参照范例2解答即可;
(3)先把![]() 看作一个整体,再参照范例2解答即可.
看作一个整体,再参照范例2解答即可.
(1)由范例1可知:不等式![]() 的解集就是数轴上到原点的距离小于5的点所对应的数组成的,如下图所示:
的解集就是数轴上到原点的距离小于5的点所对应的数组成的,如下图所示:

∴不等式![]() 的解集为:
的解集为:![]() ;
;
(2)由范例2可知:求不等式![]() 的解集就是由数轴上到原点的距离大于1,而小于3的点所对应的数组成,如下图所示:
的解集就是由数轴上到原点的距离大于1,而小于3的点所对应的数组成,如下图所示:

∴不等式![]() 的解集是
的解集是![]() 或
或![]() ;
;
(3)由(1)可知,在不等式![]() 中,当把
中,当把![]() 看作一个整体时,
看作一个整体时,![]() 的取值范围就是数轴上到原点的距离小于2的点表示的数组成的,如下图所示:
的取值范围就是数轴上到原点的距离小于2的点表示的数组成的,如下图所示:
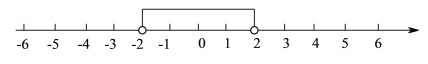
∴![]() ,
,
解得:![]()
∴不等式![]() 的解集是
的解集是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了更好地保护环境,某区污水处理厂决定购买A,B两种型号污水处理设备10台,其中每台的价格、月处理污水量如下表.已知购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.

(1)求a,b的值;
(2)某区污水处理厂决定购买污水处理设备的资金既不少于108万元也不超过110万元,问有几种购买方案?每月最多能处理污水多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1的小正方形组成的网格中,△AOB的三个顶点均在格点上,点A、B的坐标分别为(3,2)、(1,3).△AOB绕点O逆时针旋转90后得到△A1OB1.
(1)在网格中画出△A1OB1,并标上字母;
(2)点A关于O点中心对称的点的坐标为___________;
(3)点A1的坐标为________;
(4)△A1OB1的面积为_______________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小红同学在做作业时,遇到这样一道几何题:
已知:AB∥CD∥EF,∠A=110°,∠ACE=100°,过点E作EH⊥EF,垂足为E,交CD于H点.
(1)依据题意,补全图形;
(2)求∠CEH的度数.
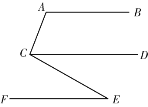
小明想了许久对于求∠CEH的度数没有思路,就去请教好朋友小丽,小丽给了他如图2所示的提示:

请问小丽的提示中理由①是 ;
提示中②是: 度;
提示中③是: 度;
提示中④是: ,理由⑤是 .
提示中⑥是 度;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠B=30°,BC=12.

(1)用尺规作图的方法作AB的垂直平分线MN,分别交BC、AB于点M、N(保留作图痕迹,不要求写作法);
(2)求第(1)题中的CM的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一条笔直的公路上有A、B两地,甲从A地去B地,乙从B地去A地然后立即原路返回B地,返回时的速度是原来的2倍,如图是甲、乙两人离B地的距离y(千米)和时间x(小时)之间的函数图象.

请根据图象回答下列问题:
(1)A、B两地的距离是千米,a=;
(2)求P的坐标,并解释它的实际意义;
(3)请直接写出当x取何值时,甲乙两人相距15千米. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径的半圆交BC于点D,过点D作EF⊥AC于点F,交AB的延长线于点E.

(1)求证:EF是⊙O的切线;
(2)当BD=3,DF= 时,求直径AB.
时,求直径AB.
相关试题

