【题目】在一条笔直的公路上有A、B两地,甲从A地去B地,乙从B地去A地然后立即原路返回B地,返回时的速度是原来的2倍,如图是甲、乙两人离B地的距离y(千米)和时间x(小时)之间的函数图象. 
请根据图象回答下列问题:
(1)A、B两地的距离是千米,a=;
(2)求P的坐标,并解释它的实际意义;
(3)请直接写出当x取何值时,甲乙两人相距15千米.
参考答案:
【答案】
(1)90;2
(2)解:设甲离B地的距离y(千米)和时间x(小时)之间的函数关系式为y=kx+b,乙离B地的距离y(千米)和时间x(小时)之间的函数关系式为y=mx+n,
将(0,90)、(3,0)代入y=kx+b中,
![]() ,解得:
,解得: ![]() ,
,
∴甲离B地的距离y和时间x之间的函数关系式为y=﹣30+90;
将(0,0)、(2,90)代入y=mx+n中,
![]() ,解得:
,解得: ![]() ,
,
∴此时y=45x(0≤x≤2);
将(2,90)、(3,0)代入y=mx+n中,
![]() ,解得:
,解得: ![]() ,
,
此时y=﹣90x+270(2≤x≤3).
∴乙离B地的距离y和时间x之间的函数关系式为y= ![]() .
.
令y=﹣30+90=45x,解得:x=1.2,
当x=1.2时,y=45x=45×1.2=54,
∴点P的坐标为(1.2,54).
点P的实际意义是:甲、乙分别从A、B两地出发,经过1.2小时相遇,这时离B地的距离为54千米
(3)解:当0≤x<1.2时,﹣30x+90﹣45x=15,
解得:x=1;
当1.2≤x<2时,45x﹣(﹣30x+90)=15,
解得:x=1.4;
当2≤x≤3时,﹣90x+270﹣(﹣30x+90)=15,
解得:x=2.75.
综上所述:当x为1、1.4或2.75时,甲乙两人相距15千米
【解析】解:(1)观察函数图象可知:A、B两地的距离是90千米, ∵乙从B地去A地然后立即原路返回B地,返回时的速度是原来的2倍,
∴a=3× ![]() =2.
=2.
故答案为:90;2.
(1)观察函数图象即可得出A、B两地的距离,由乙往返需要3小时结合返回时的速度是原来的2倍,即可求出a值;(2)观察函数图象找出点的坐标,利用待定系数法求出甲、乙离B地的距离y和时间x之间的函数关系式,令两函数关系式相等即可求出点P的坐标,再解释出它的实际意义即可;(3)分0≤x<1.2、1.2≤x<2和2≤x≤3三段,找出关于x的一元一次方程,解之即可得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小红同学在做作业时,遇到这样一道几何题:
已知:AB∥CD∥EF,∠A=110°,∠ACE=100°,过点E作EH⊥EF,垂足为E,交CD于H点.
(1)依据题意,补全图形;
(2)求∠CEH的度数.
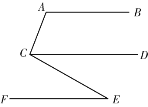
小明想了许久对于求∠CEH的度数没有思路,就去请教好朋友小丽,小丽给了他如图2所示的提示:

请问小丽的提示中理由①是 ;
提示中②是: 度;
提示中③是: 度;
提示中④是: ,理由⑤是 .
提示中⑥是 度;
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
小明在一本课外读物上看到一道有意思的数学题:例1、解不等式:
 ,根据绝对值的几何意义,到原点距离小于1的点在数轴上集中在-1和+1之间,如图:
,根据绝对值的几何意义,到原点距离小于1的点在数轴上集中在-1和+1之间,如图:
所以,该不等式的解集为-1<x<1.
因此,不等式
 的解集为x<-1或x>1.
的解集为x<-1或x>1.根据以上方法小明继续探究:例2:求不等式:
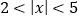 的解集,即求到原点的距离大于2小于5的点的集合就集中在这样的区域内,如图:
的解集,即求到原点的距离大于2小于5的点的集合就集中在这样的区域内,如图: 
所以,不等式
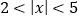 的解集为-5<x<-2或2<x<5.
的解集为-5<x<-2或2<x<5. 仿照小明的做法解决下面问题:
(1)不等式
 的解集为____________.
的解集为____________.(2)不等式
 的解集是____________.
的解集是____________.(3)求不等式
 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠B=30°,BC=12.

(1)用尺规作图的方法作AB的垂直平分线MN,分别交BC、AB于点M、N(保留作图痕迹,不要求写作法);
(2)求第(1)题中的CM的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,以AB为直径的半圆交BC于点D,过点D作EF⊥AC于点F,交AB的延长线于点E.

(1)求证:EF是⊙O的切线;
(2)当BD=3,DF= 时,求直径AB.
时,求直径AB. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,若将类似于a、b、c、d四个图的图形称做平面图,则其顶点数、边数与区域数之间存在某种关系.观察图b和表中对应的数值,探究计数的方法并作答.

(1)数一数每个图中各有多少个顶点、多少条边,这些边围出多少个区域并填表:
平面图
a
b
c
d
顶点数(S)
7
边数(M)
9
区域数(N)
3
(2)根据表中数值,写出平面图的顶点数、边数、区域数之间的一种关系为 ;
(3)如果一个平面图有20个顶点和11个区域,那么利用(2)中得出的关系可知这个平面图有 条边.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,平行四边形ABCD的对角线AC的垂直平分线与边AD、BC分别相交于点E、F.
求证:四边形AFCE是菱形.

相关试题

