【题目】小红同学在做作业时,遇到这样一道几何题:
已知:AB∥CD∥EF,∠A=110°,∠ACE=100°,过点E作EH⊥EF,垂足为E,交CD于H点.
(1)依据题意,补全图形;
(2)求∠CEH的度数.
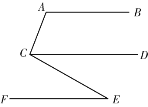
小明想了许久对于求∠CEH的度数没有思路,就去请教好朋友小丽,小丽给了他如图2所示的提示:

请问小丽的提示中理由①是 ;
提示中②是: 度;
提示中③是: 度;
提示中④是: ,理由⑤是 .
提示中⑥是 度;
参考答案:
【答案】(1)补图见解析;(2)见解析.
【解析】
(1)按照题中要求作出线段EH⊥EF于点E,交CD于点H即可;
(2)按照“小丽所给提示”的思路结合题中的已知条件根据“平行线的性质、垂直的定义”进行分析解答即可.
(1)依据题意补全图形如下图所示:
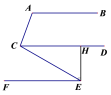 ;
;
(2)根据题意可得:
①:两直线平行,同旁内角互补;
②:70°;
③:30°;
④:∠CEF;
⑤:两直线平行,内错角相等;
⑥:60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学组织学生参加交通安全知识网络测试活动.小王对九年(3)班全体学生的测试成绩进行了统计,并将成绩分为四个等级:优秀、良好、一般、不合格,绘制成如下的统计图(不完整),

请你根据图中所给的信息解答下列问题:
(1)九年(3)班有名学生,并把折线统计图补充完整;
(2)已知该市共有12000名中学生参加了这次交通安全知识测试,请你根据该班成绩估计该市在这次测试中成绩为优秀的人数;
(3)小王查了该市教育网站发现,全市参加本次测试的学生中,成绩为优秀的有5400人,请你用所学统计知识简要说明实际优秀人数与估计人数出现较大偏差的原因;
(4)该班从成绩前3名(2男1女)的学生中随机抽取2名参加复赛,请用树状图或列表法求出抽到“一男一女”的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了更好地保护环境,某区污水处理厂决定购买A,B两种型号污水处理设备10台,其中每台的价格、月处理污水量如下表.已知购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.

(1)求a,b的值;
(2)某区污水处理厂决定购买污水处理设备的资金既不少于108万元也不超过110万元,问有几种购买方案?每月最多能处理污水多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1的小正方形组成的网格中,△AOB的三个顶点均在格点上,点A、B的坐标分别为(3,2)、(1,3).△AOB绕点O逆时针旋转90后得到△A1OB1.
(1)在网格中画出△A1OB1,并标上字母;
(2)点A关于O点中心对称的点的坐标为___________;
(3)点A1的坐标为________;
(4)△A1OB1的面积为_______________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
小明在一本课外读物上看到一道有意思的数学题:例1、解不等式:
 ,根据绝对值的几何意义,到原点距离小于1的点在数轴上集中在-1和+1之间,如图:
,根据绝对值的几何意义,到原点距离小于1的点在数轴上集中在-1和+1之间,如图:
所以,该不等式的解集为-1<x<1.
因此,不等式
 的解集为x<-1或x>1.
的解集为x<-1或x>1.根据以上方法小明继续探究:例2:求不等式:
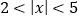 的解集,即求到原点的距离大于2小于5的点的集合就集中在这样的区域内,如图:
的解集,即求到原点的距离大于2小于5的点的集合就集中在这样的区域内,如图: 
所以,不等式
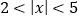 的解集为-5<x<-2或2<x<5.
的解集为-5<x<-2或2<x<5. 仿照小明的做法解决下面问题:
(1)不等式
 的解集为____________.
的解集为____________.(2)不等式
 的解集是____________.
的解集是____________.(3)求不等式
 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠B=30°,BC=12.

(1)用尺规作图的方法作AB的垂直平分线MN,分别交BC、AB于点M、N(保留作图痕迹,不要求写作法);
(2)求第(1)题中的CM的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一条笔直的公路上有A、B两地,甲从A地去B地,乙从B地去A地然后立即原路返回B地,返回时的速度是原来的2倍,如图是甲、乙两人离B地的距离y(千米)和时间x(小时)之间的函数图象.

请根据图象回答下列问题:
(1)A、B两地的距离是千米,a=;
(2)求P的坐标,并解释它的实际意义;
(3)请直接写出当x取何值时,甲乙两人相距15千米.
相关试题

