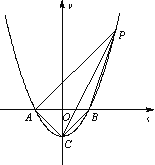
【题目】如图,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
⑴ 求![]() 、
、![]() 、
、![]() 三点的坐标.
三点的坐标.
⑵ 过点![]() 作
作![]() 交抛物线于点
交抛物线于点![]() ,求四边形
,求四边形![]() 的面积.
的面积.
⑶ 在![]() 轴上方的抛物线上是否存在一点
轴上方的抛物线上是否存在一点![]() ,过
,过![]() 作
作![]() 轴于点
轴于点![]() , 使以
, 使以![]() 、
、![]() 、
、![]() 三点为顶点的三角形与
三点为顶点的三角形与![]() 相似.若存在,请求出
相似.若存在,请求出![]() 点的坐标;否则,请说明理由.
点的坐标;否则,请说明理由.
参考答案:
【答案】(1)![]() (2)
(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)令![]() 可分别求出
可分别求出![]() 的坐标;(2)对四边形
的坐标;(2)对四边形![]() 的面积进行分割成
的面积进行分割成![]() 再分别求解;(3)假设存在,分
再分别求解;(3)假设存在,分![]() 为直角两种情况讨论,利用相似求解.
为直角两种情况讨论,利用相似求解.
试题解析:⑴![]() ,
,![]() ,
,![]()
⑵ ∵![]() ∴
∴![]()
∵![]() ∴
∴![]() .
.
过点![]() 作
作![]() 轴于
轴于![]() ,则
,则![]() 为等腰直角三角形.
为等腰直角三角形.
令![]() ,则
,则![]() .∴
.∴![]() .
.
∵点![]() 在抛物线
在抛物线![]() 上.
上.
∴![]() 解得
解得![]() ,
,![]() (不合题意,舍去)∴
(不合题意,舍去)∴![]() .
.
∴四边形![]() 的面积
的面积![]() .
.
⑶ 假设存在
∵![]() ∴
∴![]() .
.
∵![]() 轴于点
轴于点![]() ,∴
,∴![]() .
.
在![]() 中,
中,![]() ∴
∴![]()
在![]() 中,
中,![]() ∴
∴![]()
设![]() 点的横坐标为
点的横坐标为![]() ,则
,则![]()
①点![]() 在
在![]() 轴左侧时,则
轴左侧时,则![]() .
.
(ⅰ)当![]() 时,有
时,有![]() .
.
∵![]() ,
,![]() .即
.即![]() .解得
.解得![]() (舍去)
(舍去)![]() (舍去).
(舍去).
(ⅱ)当![]() 时,有
时,有![]() ,即
,即![]() .
.
解得:![]() (舍去)
(舍去)![]() . ∴
. ∴![]()
② 点![]() 在
在![]() 轴右侧时,则
轴右侧时,则![]() .
.
(ⅰ)当![]() 时有
时有![]() .
.
∵![]() ,∴
,∴![]() ,
,
解得![]() (舍去),
(舍去),![]() .∴
.∴![]()
(ⅱ)当![]() 时有
时有![]() .即
.即![]() .
.
解得:![]() (舍去)
(舍去)![]() .∴
.∴![]()
∴存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 三点为顶点的三角形与
三点为顶点的三角形与![]() 相似.
相似.
![]() 点的坐标为
点的坐标为![]() ,
,![]() ,
,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,BC=1,AC=2,把边长分别为x1,x2,x3,…,xn的n个正方形依次放入 △ABC中,请回答下列问题:
(1)按要求填表:
n
1
2
3
xn
(2)第n个正方形的边长xn= ;
(3)若m,n,p,q是正整数,且xmxn=xpxq,试判断m,n,p,q的关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一家电信公司推出两种移动电话计费方法:计费方法A是每月收月租费58元,通话时间不超过
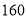 分钟的部分免费,超过
分钟的部分免费,超过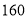 分钟的按每分钟0.25元加收通话费;计费方法B是每月收取月租费88元,通话时间不超过
分钟的按每分钟0.25元加收通话费;计费方法B是每月收取月租费88元,通话时间不超过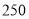 分钟的部分免费,超过
分钟的部分免费,超过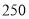 分钟的按每分钟0.20元收通话费.现在设通话时间是
分钟的按每分钟0.20元收通话费.现在设通话时间是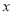 分钟.
分钟.(1)当通话时间超过
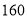 分钟时,请用含
分钟时,请用含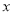 的代数式表示计费方法A的通话费用.
的代数式表示计费方法A的通话费用.(2)当通话时间超过
 分钟时,请用含
分钟时,请用含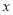 的代数式表示计费方法B的通话费用.
的代数式表示计费方法B的通话费用.(3)用计费方法A的用户一个月累计通话360分钟所需的话费,若改用计费方法B,则可通话多少分钟?
(4)请你分析,当通话时间超过多少分钟时采用计费方法B合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:4a2﹣16=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
 x2+bx-2与x轴交于A、B两点, 与y轴交于C点,且A(一1,0).
x2+bx-2与x轴交于A、B两点, 与y轴交于C点,且A(一1,0).⑴求抛物线的解析式及顶点D的坐标;
⑵判断△ABC的形状,证明你的结论;
⑶点M(m,0)是x轴上的一个动点,当CM+DM的值最小时,求m的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司派出甲车前往某地完成任务,此时,有一辆流动加油车与他同时出发,且在同一条公路上匀速行驶(速度保持不变).为了确定汽车的位置,我们用OX表示这条公路,原点O为零千米路标,并作如下约定:速度为正,表示汽车向数轴的正方向行驶;速度为负,表示汽车向数轴的负方向行驶;速度为零,表示汽车静止.行程为正,表示汽车位于零千米的右侧;行程为负,表示汽车位于零千米的左侧;行程为零,表示汽车位于零千米处.两车行程记录如表:

由上面表格中的数据,解决下列问题:
(1)甲车开出7小时时的位置为 km,流动加油车出发位置为 km;
(2)当两车同时开出x小时时,甲车位置为 km,流动加油车位置为 km (用x的代数式表示);
(3)甲车出发前由于未加油,汽车启动后司机才发现油箱内汽油仅够行驶3小时,问:甲车连续行驶3小时后,能否立刻获得流动加油车的帮助?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】长为10, 7, 5, 3的四根木条,选其中三根首尾顺次相连接组成三角形,选法有( )
A. 1种 B. 2种 C. 3种 D. 4种
相关试题

