【题目】一家电信公司推出两种移动电话计费方法:计费方法A是每月收月租费58元,通话时间不超过![]() 分钟的部分免费,超过
分钟的部分免费,超过![]() 分钟的按每分钟0.25元加收通话费;计费方法B是每月收取月租费88元,通话时间不超过
分钟的按每分钟0.25元加收通话费;计费方法B是每月收取月租费88元,通话时间不超过![]() 分钟的部分免费,超过
分钟的部分免费,超过![]() 分钟的按每分钟0.20元收通话费.现在设通话时间是
分钟的按每分钟0.20元收通话费.现在设通话时间是![]() 分钟.
分钟.
(1)当通话时间超过![]() 分钟时,请用含
分钟时,请用含![]() 的代数式表示计费方法A的通话费用.
的代数式表示计费方法A的通话费用.
(2)当通话时间超过![]() 分钟时,请用含
分钟时,请用含![]() 的代数式表示计费方法B的通话费用.
的代数式表示计费方法B的通话费用.
(3)用计费方法A的用户一个月累计通话360分钟所需的话费,若改用计费方法B,则可通话多少分钟?
(4)请你分析,当通话时间超过多少分钟时采用计费方法B合算?
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)350;(4)通话时间超400分钟时,采用计费方法B合算。
;(3)350;(4)通话时间超400分钟时,采用计费方法B合算。
【解析】试题分析:(1)根据计费方法A出列代数式表示出通话费用即可;(2)根据计费方法B列出代数式表示出通话费用即可;(3)根据用计费方法A的用户一个月累计通话360分钟所需的话费=计费方法B的通话费用列出方程,求出方程的解即可得到结果;(4)由于超过一定时间后,B的计费方式每分钟费用小于A的计费方式,因此时间越多,B的计费方式越合算,根据题意列出方程,求出方程的解即可得到结果.
试题解析:(1)A:58+0.25(x-160)=0.25x+18;
(2)B:88+0.2(x-250)=0.2x+38;
(3)由题得:0.2x+38=0.25×360+18,解得:x=350,则改用计费方法B,可通话350分钟;
(4)由于超过一定时间后,B的计费方式每分钟费用小于A的计费方式,因此时间越多,B的计费方式越合算,当用x分钟时,两种计费方式所需费用一样,得0.2x+38=0.25x+18,解得:x=400,答:当通话时间超400分钟时,采用计费方法B合算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P在x轴上,且
 ,
, ,点M也在x轴上,在OA上找点N,以P、M、N为顶点作正方形,则ON= (如结果中有根号,请保留根号).
,点M也在x轴上,在OA上找点N,以P、M、N为顶点作正方形,则ON= (如结果中有根号,请保留根号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=DC,AD=BC,E,F在DB上两点且BF=DE,若∠AEB=120°,∠ADB=30°,则∠BCF= ( )

A. 150° B. 40° C. 80° D. 90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,BC=1,AC=2,把边长分别为x1,x2,x3,…,xn的n个正方形依次放入 △ABC中,请回答下列问题:
(1)按要求填表:
n
1
2
3
xn
(2)第n个正方形的边长xn= ;
(3)若m,n,p,q是正整数,且xmxn=xpxq,试判断m,n,p,q的关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:4a2﹣16=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线
 与
与 轴交于
轴交于 、
、 两点,与
两点,与 轴交于点
轴交于点 .
.⑴ 求
 、
、 、
、 三点的坐标.
三点的坐标.⑵ 过点
 作
作 交抛物线于点
交抛物线于点 ,求四边形
,求四边形 的面积.
的面积.⑶ 在
 轴上方的抛物线上是否存在一点
轴上方的抛物线上是否存在一点 ,过
,过 作
作 轴于点
轴于点 , 使以
, 使以 、
、 、
、 三点为顶点的三角形与
三点为顶点的三角形与 相似.若存在,请求出
相似.若存在,请求出 点的坐标;否则,请说明理由.
点的坐标;否则,请说明理由.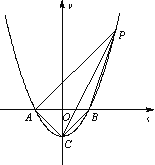
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=
 x2+bx-2与x轴交于A、B两点, 与y轴交于C点,且A(一1,0).
x2+bx-2与x轴交于A、B两点, 与y轴交于C点,且A(一1,0).⑴求抛物线的解析式及顶点D的坐标;
⑵判断△ABC的形状,证明你的结论;
⑶点M(m,0)是x轴上的一个动点,当CM+DM的值最小时,求m的值.

相关试题

