搜索
【题目】下列运算正确的是（ ）
A.aa2=a2
B.（ab）2=ab
C.3﹣1= 
D.
参考答案：
【答案】C
【解析】解：A、原式=a3，所以A选项不符合题意；
B、原式=a2b2，所以B选项不符合题意；
C、原式= 
，所以C选项符合题意；
D、原式=2 
，所以D选项不符合题意．
所以答案是：C．
【考点精析】关于本题考查的整数指数幂的运算性质和同底数幂的乘法，需要了解aman=am+n(m、n是正整数)；（am）n=amn(m、n是正整数)；(ab)n=anbn(n是正整数)；am/an=am-n(a不等于0，m、n为正整数）；（a/b）n=an/bn(n为正整数)；同底数幂的乘法法则aman=am+n(m,n都是正数)才能得出正确答案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，∠A＝40°
（1）如图1，若两内角∠ABC、∠ACB的角平分线交于点P，则∠P＝ ，∠A与∠P之间的数量关系是 ．为什么有这样的关系？请证明它；
（2）如图2，若内角∠ABC、外角∠ACE的角平分线交于点P，则∠P＝ ，∠A与∠P之间的数量关系是 ；
（3）如图3，若两外角∠EBC、∠FCB的角平分线交于点P，则∠P＝ ，∠A与∠P之间的数量关系是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图是某学校草场一角，在长为b米，宽为a米的长方形场地中间，有并排两个大小一样的篮球场，两个篮球场中间以及篮球场与长方形场地边沿的距离都为c米．
（1）用代数式表示这两个篮球场的占地面积．
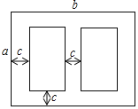
（2）当a=30，b=40，c=3时，计算出一个篮球场的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】定义：对于给定的两个函数，任取自变量x的一个值，当x＜0时，它们对应的函数值互为相反数；当x≥0时，它们对应的函数值相等，我们称这样的两个函数互为相关函数．例如：一次函数y=x﹣1，它的相关函数为y=
．
（1）已知点A（﹣5，8）在一次函数y=ax﹣3的相关函数的图象上，求a的值；
（2）已知二次函数y=﹣x2+4x﹣
．①当点B（m， 
）在这个函数的相关函数的图象上时，求m的值；
②当﹣3≤x≤3时，求函数y=﹣x2+4x﹣ 的相关函数的最大值和最小值；
（3）在平面直角坐标系中，点M，N的坐标分别为（﹣ ，1），（ 
，1），连结MN．直接写出线段MN与二
次函数y=﹣x2+4x+n的相关函数的图象有两个公共点时n的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知，△ABC是边长3cm的等边三角形．动点P以1cm/s的速度从点A出发，沿线段AB向点B运动．
（1）如图1，设点P的运动时间为t（s），那么t＝ （s）时，△PBC是直角三角形；
（2）如图2，若另一动点Q从点B出发，沿线段BC向点C运动，如果动点P、Q都以1cm/s的速度同时出发．设运动时间为t（s），那么t为何值时，△PBQ是直角三角形？
（3）如图3，若另一动点Q从点C出发，沿射线BC方向运动．连接PQ交AC于D．如果动点P、Q都以1cm/s的速度同时出发．设运动时间为t（s），那么t为何值时，△DCQ是等腰三角形？
（4）如图4，若另一动点Q从点C出发，沿射线BC方向运动．连接PQ交AC于D，连接PC．如果动点P、Q都以1cm/s的速度同时出发．请你猜想：在点P、Q的运动过程中，△PCD和△QCD的面积有什么关系？并说明理由．
-
科目： 来源： 题型：
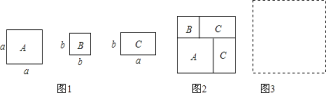
查看答案和解析>>【题目】现有若干张如图1所示的正方形纸片A，B和长方形纸片C．
（1）小王利用这些纸片拼成了如图2的一个新正方形，通过用两种不同的方法计算新正方形面积，由此，他得到了一个等式：______ ；
（2）小王再取其中的若干张纸片（三种纸片都要取到）拼成一个面积为a2+3ab+nb2的长方形，则n可取的正整数值是______ ，并请你在图3位置画出拼成的长方形；
（3）根据拼图经验，请将多项式a2+5ab+4b2分解因式．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB=30，C为射线AB上一点，BC比AC的4倍少20，P，Q两点分别从A，B两点同时出发．分别以2单位/秒和1单位/秒的速度在射线AB上沿AB方向运动，运动时间为t秒，M为BP的中点，N为QM的中点，以下结论：①BC=2AC；②运动过程中，QM的长度保持不变；③AB=4NQ；④当BQ=PB时，t=12，其中正确结论的个数是（ ）
A. 1B. 2C. 3D. 4
相关试题
