【题目】定义:对于给定的两个函数,任取自变量x的一个值,当x<0时,它们对应的函数值互为相反数;当x≥0时,它们对应的函数值相等,我们称这样的两个函数互为相关函数.例如:一次函数y=x﹣1,它的相关函数为y= ![]() .
.
(1)已知点A(﹣5,8)在一次函数y=ax﹣3的相关函数的图象上,求a的值;
(2)已知二次函数y=﹣x2+4x﹣ ![]() .①当点B(m,
.①当点B(m, ![]() )在这个函数的相关函数的图象上时,求m的值;
)在这个函数的相关函数的图象上时,求m的值;
②当﹣3≤x≤3时,求函数y=﹣x2+4x﹣ ![]() 的相关函数的最大值和最小值;
的相关函数的最大值和最小值;
(3)在平面直角坐标系中,点M,N的坐标分别为(﹣ ![]() ,1),(
,1),( ![]() ,1),连结MN.直接写出线段MN与二
,1),连结MN.直接写出线段MN与二
次函数y=﹣x2+4x+n的相关函数的图象有两个公共点时n的取值范围.
参考答案:
【答案】
(1)解:函数y=ax﹣3的相关函数为y= ![]() ,将点A(﹣5,8)代入y=﹣ax+3得:5a+3=8,解得:a=1.
,将点A(﹣5,8)代入y=﹣ax+3得:5a+3=8,解得:a=1.
(2)解:二次函数y=﹣x2+4x﹣ ![]() 的相关函数为y=
的相关函数为y= 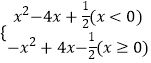
①当m<0时,将B(m, ![]() )代入y=x2﹣4x+
)代入y=x2﹣4x+ ![]() 得m2﹣4m+
得m2﹣4m+ ![]() =
= ![]() ,解得:m=2+
,解得:m=2+ ![]() (舍去)或m=2﹣
(舍去)或m=2﹣ ![]() .
.
当m≥0时,将B(m, ![]() )代入y=﹣x2+4x﹣
)代入y=﹣x2+4x﹣ ![]() 得:﹣m2+4m﹣
得:﹣m2+4m﹣ ![]() =
= ![]() ,解得:m=2+
,解得:m=2+ ![]() 或m=2﹣
或m=2﹣ ![]() .
.
综上所述:m=2﹣ ![]() 或m=2+
或m=2+ ![]() 或m=2﹣
或m=2﹣ ![]() .
.
②当﹣3≤x<0时,y=x2﹣4x+ ![]() ,抛物线的对称轴为x=2,此时y随x的增大而减小,
,抛物线的对称轴为x=2,此时y随x的增大而减小,
∴此时y的最大值为 ![]() .
.
当0≤x≤3时,函数y=﹣x2+4x﹣ ![]() ,抛物线的对称轴为x=2,当x=0有最小值,最小值为﹣
,抛物线的对称轴为x=2,当x=0有最小值,最小值为﹣ ![]() ,当x=2时,有最大值,最大值y=
,当x=2时,有最大值,最大值y= ![]() .
.
综上所述,当﹣3≤x≤3时,函数y=﹣x2+4x﹣ ![]() 的相关函数的最大值为
的相关函数的最大值为 ![]() ,最小值为﹣
,最小值为﹣ ![]() ;
;
(3)解:如图1所示:线段MN与二次函数y=﹣x2+4x+n的相关函数的图象恰有1个公共点.
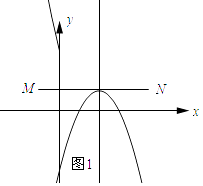
所以当x=2时,y=1,即﹣4+8+n=1,解得n=﹣3.
如图2所示:线段MN与二次函数y=﹣x2+4x+n的相关函数的图象恰有3个公共点
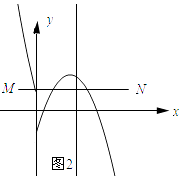
∵抛物线y=x2﹣4x﹣n与y轴交点纵坐标为1,
∴﹣n=1,解得:n=﹣1.
∴当﹣3<n≤﹣1时,线段MN与二次函数y=﹣x2+4x+n的相关函数的图象恰有2个公共点.
如图3所示:线段MN与二次函数y=﹣x2+4x+n的相关函数的图象恰有3个公共点.
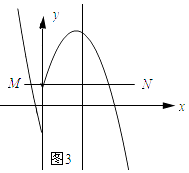
∵抛物线y=﹣x2+4x+n经过点(0,1),
∴n=1.
如图4所示:线段MN与二次函数y=﹣x2+4x+n的相关函数的图象恰有2个公共点.
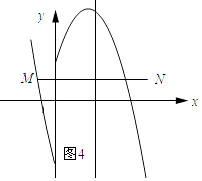
∵抛物线y=x2﹣4x﹣n经过点M(﹣ ![]() ,1),
,1),
∴ ![]() +2﹣n=1,解得:n=
+2﹣n=1,解得:n= ![]() .
.
∴1<n≤ ![]() 时,线段MN与二次函数y=﹣x2+4x+n的相关函数的图象恰有2个公共点.
时,线段MN与二次函数y=﹣x2+4x+n的相关函数的图象恰有2个公共点.
综上所述,n的取值范围是﹣3<n≤﹣1或1<n≤ ![]() .
.
【解析】(1)因为点在函数图像上,把点的坐标代入解析式;(2)对于点B(m,![]() ),由于m不知正负,因此需分类讨论;(2)由于﹣3≤x≤3有正又有负,因此需分段:3≤x<0和0≤x≤3,分别对应着相关函数的两段解析式,分别求最大值和最小值,最后比较两段函数的最大值的较大着作为整个函数的最大值;(3)需数形结合,按照抛物线与y轴的交点由低到高,可推出﹣3<n≤﹣1或1<n≤
),由于m不知正负,因此需分类讨论;(2)由于﹣3≤x≤3有正又有负,因此需分段:3≤x<0和0≤x≤3,分别对应着相关函数的两段解析式,分别求最大值和最小值,最后比较两段函数的最大值的较大着作为整个函数的最大值;(3)需数形结合,按照抛物线与y轴的交点由低到高,可推出﹣3<n≤﹣1或1<n≤ ![]() .
.
【考点精析】根据题目的已知条件,利用二次函数的性质的相关知识可以得到问题的答案,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在Rt△ABC中,∠C=90°,沿过B点的一条直线BE折叠这个三角形, 使C点与AB边上的一点D重合.
(1)当∠A满足什么条件时,点D恰为AB的中点?写出一个你认为适当的条件,并利用此条件证明D为AB的中点;
(2)在(1)的条件下,若DE=1,求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠A=40°
(1)如图1,若两内角∠ABC、∠ACB的角平分线交于点P,则∠P= ,∠A与∠P之间的数量关系是 .为什么有这样的关系?请证明它;
(2)如图2,若内角∠ABC、外角∠ACE的角平分线交于点P,则∠P= ,∠A与∠P之间的数量关系是 ;
(3)如图3,若两外角∠EBC、∠FCB的角平分线交于点P,则∠P= ,∠A与∠P之间的数量关系是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某学校草场一角,在长为b米,宽为a米的长方形场地中间,有并排两个大小一样的篮球场,两个篮球场中间以及篮球场与长方形场地边沿的距离都为c米.
(1)用代数式表示这两个篮球场的占地面积.
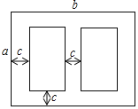
(2)当a=30,b=40,c=3时,计算出一个篮球场的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.aa2=a2
B.(ab)2=ab
C.3﹣1=
D.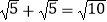
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,△ABC是边长3cm的等边三角形.动点P以1cm/s的速度从点A出发,沿线段AB向点B运动.
(1)如图1,设点P的运动时间为t(s),那么t= (s)时,△PBC是直角三角形;
(2)如图2,若另一动点Q从点B出发,沿线段BC向点C运动,如果动点P、Q都以1cm/s的速度同时出发.设运动时间为t(s),那么t为何值时,△PBQ是直角三角形?
(3)如图3,若另一动点Q从点C出发,沿射线BC方向运动.连接PQ交AC于D.如果动点P、Q都以1cm/s的速度同时出发.设运动时间为t(s),那么t为何值时,△DCQ是等腰三角形?
(4)如图4,若另一动点Q从点C出发,沿射线BC方向运动.连接PQ交AC于D,连接PC.如果动点P、Q都以1cm/s的速度同时出发.请你猜想:在点P、Q的运动过程中,△PCD和△QCD的面积有什么关系?并说明理由.

-
科目: 来源: 题型:
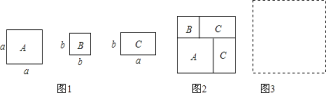
查看答案和解析>>【题目】现有若干张如图1所示的正方形纸片A,B和长方形纸片C.
(1)小王利用这些纸片拼成了如图2的一个新正方形,通过用两种不同的方法计算新正方形面积,由此,他得到了一个等式:______ ;
(2)小王再取其中的若干张纸片(三种纸片都要取到)拼成一个面积为a2+3ab+nb2的长方形,则n可取的正整数值是______ ,并请你在图3位置画出拼成的长方形;
(3)根据拼图经验,请将多项式a2+5ab+4b2分解因式.
相关试题

