【题目】如图,AB=30,C为射线AB上一点,BC比AC的4倍少20,P,Q两点分别从A,B两点同时出发.分别以2单位/秒和1单位/秒的速度在射线AB上沿AB方向运动,运动时间为t秒,M为BP的中点,N为QM的中点,以下结论:①BC=2AC;②运动过程中,QM的长度保持不变;③AB=4NQ;④当BQ=PB时,t=12,其中正确结论的个数是( )

A. 1B. 2C. 3D. 4
参考答案:
【答案】C
【解析】
根据AB=30,BC比AC的4倍少20可分别求出AC与BC的长度;分别表示出BM、BQ,由QM=BM+BQ即可得QM的值;由N为QM的中点得NQ=![]() QM可得NQ的值;当BQ=PB时,可得30-2t=t,此时t=10秒,综上所述即可得结论.
QM可得NQ的值;当BQ=PB时,可得30-2t=t,此时t=10秒,综上所述即可得结论.
∵AB=30,BC比AC的4倍少20,
∴AC=10,BC=20,
∴BC=2AC,①正确;
∵P、Q两点的运动速度分别为2单位/秒和1单位/秒的速度,
∴BP=30-2t,BQ=t,
∵M为BP的中点,N为QM的中点,
∴PM=MB=15-t,MQ=MB+BQ=15,NQ=7.5,
∴运动过程中,QM的长度保持不变,AB=4NQ,②③正确;
∵PB=30-2t,BQ=t,当BQ=PB时,,
∴30-2t=t,
解方程得:t=10,④错误;
∴①②③项结论正确.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.aa2=a2
B.(ab)2=ab
C.3﹣1=
D.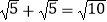
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,△ABC是边长3cm的等边三角形.动点P以1cm/s的速度从点A出发,沿线段AB向点B运动.
(1)如图1,设点P的运动时间为t(s),那么t= (s)时,△PBC是直角三角形;
(2)如图2,若另一动点Q从点B出发,沿线段BC向点C运动,如果动点P、Q都以1cm/s的速度同时出发.设运动时间为t(s),那么t为何值时,△PBQ是直角三角形?
(3)如图3,若另一动点Q从点C出发,沿射线BC方向运动.连接PQ交AC于D.如果动点P、Q都以1cm/s的速度同时出发.设运动时间为t(s),那么t为何值时,△DCQ是等腰三角形?
(4)如图4,若另一动点Q从点C出发,沿射线BC方向运动.连接PQ交AC于D,连接PC.如果动点P、Q都以1cm/s的速度同时出发.请你猜想:在点P、Q的运动过程中,△PCD和△QCD的面积有什么关系?并说明理由.

-
科目: 来源: 题型:
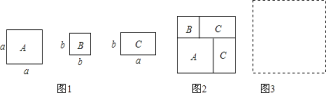
查看答案和解析>>【题目】现有若干张如图1所示的正方形纸片A,B和长方形纸片C.
(1)小王利用这些纸片拼成了如图2的一个新正方形,通过用两种不同的方法计算新正方形面积,由此,他得到了一个等式:______ ;
(2)小王再取其中的若干张纸片(三种纸片都要取到)拼成一个面积为a2+3ab+nb2的长方形,则n可取的正整数值是______ ,并请你在图3位置画出拼成的长方形;
(3)根据拼图经验,请将多项式a2+5ab+4b2分解因式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司有A、B两种客车,它们的载客量和租金如下表,星星中学根据实际情况,计划用A、B型车共5辆,同时送七年级师生到校基地参加社会实践活动.
A
B
载客量(人/辆)
40
20
租金(元/辆)
200
150
(1)若要保证租金费用不超过980元,请问该学校有哪几种租车方案?
(2)在(1)的条件下,若七年级师生共有150人,问哪种租车方案最省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,其中A,B,C三地在同一直线上,D地在A地北偏东30°方向、在C地北偏西45°方向.C 地在A地北偏东75°方向.且BD=BC=30cm.从A地到D地的距离是( )

A.30 m
m
B.20 m
m
C.30 m
m
D.15 m
m -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,点D是AB边的中点,过D作DE⊥BC于点E,点P是边BC上的一个动点,AP与CD相交于点Q.当AP+PD的值最小时,AQ与PQ之间的数量关系是( )

A.AQ= PQ
PQ
B.AQ=3PQ
C.AQ= PQ
PQ
D.AQ=4PQ
相关试题

