搜索
【题目】如图，已知AD是△ABC的角平分线，CE是△ABC的高，AD与CE相交于点P，∠BAC=66°，∠BCE=40°，求∠ADC和∠APC的度数．
参考答案：
【答案】123°
【解析】
根据角平分线的定义可得∠BAD=∠CAD=
∠BAC=33°，再根据直角三角形两锐角互余求出∠B，然后根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可求出∠ADC，根据三角形的一个外角等于与它不相邻的两个内角的和可得∠APC=∠ADC+∠BCE．
∵AD是△ABC的角平分线，∠BAC=66°，
∴∠BAD=∠CAD= ∠BAC=33°，
∵CE是△ABC的高，
∴∠BEC=90°，
∵∠BCE=40°，
∴∠B=50°，
∴∠ADC=∠BAD+∠B=33°+50°=83°；
∠APC=∠ADC+∠BCE
=83°+40°
=123°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知
、
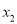是关于
的方程
的两个不相等的实数根.(1)求实数
的取值范围;(2)已知等腰
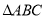的一边长为7，若
、
恰好是
另外两边长，求这个三角形的周长. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，等腰
中，
，点
是边
上不与点
、
重合的一个动点，直线
垂直平分
，垂足为
．当
是等腰三角形时，
的长为_______．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下面是某同学对多项式
进行因式分解的过程．解：设
，原式
（第一步）
（第二步）
（第三步）
．（第四步）请你回答下列问题：
（1）该同学第二步到第三步运用了因式分解的_______；
A．提公因式法 B．平方差公式
C．两数和的完全平方公式 D．两数差的完全平方公式
（2）该同学因式分解的结果不彻底，请直接写出因式分解的最后结果_______；
（3）仿照以上方法因式分解：
． -
科目： 来源： 题型：
查看答案和解析>>【题目】（本题6分）如图，已知△ABC，∠C=Rt∠，AC<BC，D为BC上一点，且到A，B两点的距离相等．
（1）用直尺和圆规，作出点D的位置（不写作法，保留作图痕迹）；
（2）连结AD，若∠B=37°，求∠CAD的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读以下材料，并按要求完成相应的任务．
在初中数学课本中重点介绍了提公因式法和运用公式法两种因式
分解的方法，其中运用公式法即运用平方差公式：
和完全平方公式：
进行分解因式，能运用完全平方公式分解因式的多项式必须是三项式，其中有两项能写成两个数（或式）的平方和的形式，另一项是这两个数（或式）的积的2倍．当一个二次三项式不能直接能运用完全平方公式分解因式时，可应用下面方法分解因式，先将多项式
变形为
的形式，我们把这样的变形方法叫做多项式的配方法．再运用多项式的配方法及平方差公式能对一些多项式进行分解因式．例如：
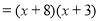．根据以上材料，完成相应的任务：
（1）利用“多项式的配方法”将
化成的形式为_______；（2）请你利用上述方法因式分解：
①
； ②
． -
科目： 来源： 题型：
查看答案和解析>>【题目】综合与实践
如图1，
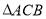和
都是等腰直角三角形，其中
，点
在线段
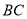上．
操作发现：如图2，保持点
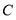不动，绕点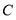按顺时针旋转角度
（
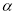），连接
与
．
（1）猜想线段
，之间的数量关系，并说明理由；拓展探究：如图3，
绕点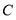继续按顺时针旋转，当点
，，
在同一直线上时，过点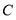作
，垂足为
．
（2）求
的度数；（3）直接写出线段
，
，之间的的数量关系．
相关试题
