【题目】综合与实践
如图1,![]() 和
和![]() 都是等腰直角三角形,其中
都是等腰直角三角形,其中![]() ,点
,点![]() 在线段
在线段![]() 上.
上.

操作发现:如图2,保持点![]() 不动,
不动,![]() 绕点
绕点![]() 按顺时针旋转角度
按顺时针旋转角度![]() (
(![]() ),连接
),连接![]() 与
与![]() .
.

(1)猜想线段![]() ,
,![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
拓展探究:如图3,![]() 绕点
绕点![]() 继续按顺时针旋转,当点
继续按顺时针旋转,当点![]() ,
,![]() ,
,![]() 在同一直线上时,过点
在同一直线上时,过点![]() 作
作![]() ,垂足为
,垂足为![]() .
.

(2)求![]() 的度数;
的度数;
(3)直接写出线段![]() ,
,![]() ,
,![]() 之间的的数量关系.
之间的的数量关系.
参考答案:
【答案】(1)![]() ,理由见解析;(2)90
,理由见解析;(2)90![]() ;(3)
;(3)![]()
【解析】
(1)根据等腰三角形的性质得到![]() ,
,![]() ,证明
,证明![]() ,即可得到结论;
,即可得到结论;
(2)根据全等的性质得到![]() ,再根据
,再根据![]() 求出答案;
求出答案;
(3)根据等腰直角三角形的性质得到DM=EM=CM,根据三角形全等得到AD=BE,由此得到答案.
解:(1)![]() .
.
理由如下:
∵![]() 和
和![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,即
,即![]() .
.
在![]() 和
和![]() 中,
中,

∴![]() .
.
∴![]() .
.
(2)∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
由(1)知,![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)![]() ,
,
∵△CDE是等腰直角三角形,![]() ,CM⊥DE,
,CM⊥DE,
∴DM=EM=CM,即DE=2CM,
∵![]() ,
,
∴AD=BE,
∵AE=AD+DE=2CM+BE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD是△ABC的角平分线,CE是△ABC的高,AD与CE相交于点P,∠BAC=66°,∠BCE=40°,求∠ADC和∠APC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题6分)如图,已知△ABC,∠C=Rt∠,AC<BC,D为BC上一点,且到A,B两点的距离相等.

(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若∠B=37°,求∠CAD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读以下材料,并按要求完成相应的任务.
在初中数学课本中重点介绍了提公因式法和运用公式法两种因式
分解的方法,其中运用公式法即运用平方差公式:
 和完全平方公式:
和完全平方公式: 进行分解因式,能运用完全平方公式分解因式的多项式必须是三项式,其中有两项能写成两个数(或式)的平方和的形式,另一项是这两个数(或式)的积的2倍.当一个二次三项式不能直接能运用完全平方公式分解因式时,可应用下面方法分解因式,先将多项式
进行分解因式,能运用完全平方公式分解因式的多项式必须是三项式,其中有两项能写成两个数(或式)的平方和的形式,另一项是这两个数(或式)的积的2倍.当一个二次三项式不能直接能运用完全平方公式分解因式时,可应用下面方法分解因式,先将多项式
 变形为
变形为 的形式,我们把这样的变形方法叫做多项式
的形式,我们把这样的变形方法叫做多项式 的配方法.再运用多项式的配方法及平方差公式能对一些多项式进行分解因式.
的配方法.再运用多项式的配方法及平方差公式能对一些多项式进行分解因式.例如:




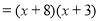 .
.根据以上材料,完成相应的任务:
(1)利用“多项式的配方法”将
 化成
化成 的形式为_______;
的形式为_______;(2)请你利用上述方法因式分解:
①
 ; ②
; ② .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC中,AC=BC,以BC为直径的⊙O交AB于点D,过点D作DE⊥AC于点E,交BC的延长线于点F.
求证:
(1)AD=BD;
(2)DF是⊙O的切线.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰△ABC顶角∠A=36°.
(1)尺规作图:在AC上作一点D,使AD=BD;(保留作图痕迹,不必写作法和证明)
(2)求证:△BCD是等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形网格图中建立一直角坐标系,一条圆弧经过网格点A、B、C,请在网格中进行下列操作:

(1)请在图中确定该圆弧所在圆心D点的位置,D点坐标为 ;
(2)连接AD、CD,求⊙D的半径及扇形DAC的圆心角度数;
(3)若扇形DAC是某一个圆锥的侧面展开图,求该圆锥的底面半径.
相关试题

