【题目】如图,等腰![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 上不与点
上不与点![]() 、
、![]() 重合的一个动点,直线
重合的一个动点,直线![]() 垂直平分
垂直平分![]() ,垂足为
,垂足为![]() .当
.当![]() 是等腰三角形时,
是等腰三角形时,![]() 的长为_______.
的长为_______.

参考答案:
【答案】![]() 或
或![]()
【解析】
根据勾股定理求出BC,分两种情况:①当AF=CF时,∠FAC=∠C=45°,∠AFC=90°,根据等腰直角三角形的性质得出BF=CF=![]() BC=1,根据直线
BC=1,根据直线![]() 垂直平分
垂直平分![]() ,垂足为
,垂足为![]() ,求出BD=
,求出BD=![]() BF=
BF=![]() ;②当CF=CA=
;②当CF=CA=![]() 时,BF=BC-CF=2-
时,BF=BC-CF=2-![]() ,根据直线
,根据直线![]() 垂直平分
垂直平分![]() ,垂足为
,垂足为![]() ,求出BD=
,求出BD=![]() BF=
BF=![]() .
.
∵等腰![]() 中,
中,![]() ,
,
∴BC=2,∠B=∠C=45°,
分两种情况:
①当AF=CF时,∠FAC=∠C=45°,
∴∠AFC=90°,
∴AF⊥BC,
∴BF=CF=![]() BC=1,
BC=1,
∵直线![]() 垂直平分
垂直平分![]() ,垂足为
,垂足为![]() ,
,
∴BD=![]() BF=
BF=![]() ;
;
②当CF=CA=![]() 时,BF=BC-CF=2-
时,BF=BC-CF=2-![]() ,
,
∵直线![]() 垂直平分
垂直平分![]() ,垂足为
,垂足为![]() ,
,
∴BD=![]() BF=
BF=![]() ,
,
故答案为:![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图(1),如果AB∥CD∥EF. 那么∠BAC+∠ACE+∠CEF=360°.
老师要求学生在完成这道教材上的题目后,尝试对图形进行变式,继续做拓展探究,看看有什么新发现?
(1)小华首先完成了对这道题的证明,在证明过程中她用到了平行线的一条性质,小华用到的平行线性质可能是______________.
(2)接下来,小华用《几何画板》对图形进行了变式,她先画了两条平行线AB,EF,然后在平行线间画了一点C,连接AC,EC后,用鼠标拖动点C,分别得到了图(2)(3)(4),小华发现图(3)正是上面题目的原型,于是她由上题的结论猜想到图(2)和(4)中的∠BAC,∠ACE与∠CEF之间也可能存在着某种数量关系.然后,她利用《几何画板》的度量与计算功能,找到了这三个角之间的数量关系.
请你在小华操作探究的基础上,继续完成下面的问题:
①猜想:图(2)中∠BAC,∠ACE与∠CEF之间的数量关系: .
②补全图(4),并直接写出图中∠BAC,∠ACE与∠CEF之间的数量关系: . (3)小华继续探究:如图(5),若直线AB与直线EF不平行,点G,H分别在直线AB、直线EF上,点C在两直线外,连接CG,CH,GH,且GH同时平分∠BGC和∠FHC,请探索∠AGC,∠GCH与∠CHE之间的数量关系?并说明理由.


-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》是中国古代数学专著,在数学上有其独到的成就,不仅最早提到了分数问题,也首先记录了“盈不足”等问题.如有一道阐述“盈不足”的问题,原文如下:今有共买鸡,人出九,盈十一;人出六,不足十六.问人数、鸡价各几何?译文为:现有若干人合伙出钱买鸡,如果每人出9文钱,就会多11文钱;如果每人出6文钱,又会缺16文钱.问买鸡的人数、鸡的价格各是多少?请解答上述问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 、
、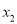 是关于
是关于 的方程
的方程 的两个不相等的实数根.
的两个不相等的实数根.(1)求实数
 的取值范围;
的取值范围;(2)已知等腰
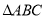 的一边长为7,若
的一边长为7,若 、
、 恰好是
恰好是 另外两边长,求这个三角形的周长.
另外两边长,求这个三角形的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】下面是某同学对多项式
 进行因式分解的过程.
进行因式分解的过程.解:设
 ,
,原式
 (第一步)
(第一步) (第二步)
(第二步) (第三步)
(第三步) .(第四步)
.(第四步)请你回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______;
A.提公因式法 B.平方差公式
C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学因式分解的结果不彻底,请直接写出因式分解的最后结果_______;
(3)仿照以上方法因式分解:
 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD是△ABC的角平分线,CE是△ABC的高,AD与CE相交于点P,∠BAC=66°,∠BCE=40°,求∠ADC和∠APC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题6分)如图,已知△ABC,∠C=Rt∠,AC<BC,D为BC上一点,且到A,B两点的距离相等.

(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);
(2)连结AD,若∠B=37°,求∠CAD的度数.
相关试题

