【题目】如图,点A,B,C分别是⊙O上的点,∠B=60°,AC=3,CD是⊙O的直径,P是CD延长线上的一点,且AP=AC.
(1)求证:AP是⊙O的切线;
(2)求PD的长.
参考答案:
【答案】
(1)解:证明:连接OA.

∵∠B=60°,
∴∠AOC=2∠B=120°,
又∵OA=OC,
∴∠ACP=∠CAO=30°,
∴∠AOP=60°,
∵AP=AC,
∴∠P=∠ACP=30°,
∴∠OAP=90°,
∴OA⊥AP,
∴AP是⊙O的切线,
(2)解:连接AD.
∵CD是⊙O的直径,
∴∠CAD=90°,
∴AD=ACtan30°=3× ![]() =
= ![]() ,
,
∵∠ADC=∠B=60°,
∴∠PAD=∠ADC﹣∠P=60°﹣30°=30°,
∴∠P=∠PAD,
∴PD=AD= ![]() .
.
【解析】(1)连接OA,由直径所对的圆周角为90°可得到∠DAC=90°,故此可得到∠ACP=∠APC=30°,然后再求得∠AOP=60°,从而得到∠PAO=90°;(2)由直径所对的圆周角为90°可得到∠DAC=90°,然后利用三角函数与等腰三角形的判定定理可求得PD的长.
【考点精析】利用圆周角定理和切线的判定定理对题目进行判断即可得到答案,需要熟知顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.
(1)在方程①3x﹣1=0,②
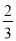 x+1=0,③x﹣(3x+1)=﹣5中,不等式组
x+1=0,③x﹣(3x+1)=﹣5中,不等式组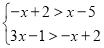 的关联方程是 ;(填序号)
的关联方程是 ;(填序号)(2)若不等式组
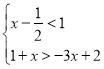 的一个关联方程的根是整数,则这个关联方程可以是 ;(写出一个即可)
的一个关联方程的根是整数,则这个关联方程可以是 ;(写出一个即可)(3)若方程3﹣x=2x,3+x=2(x+
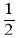 )都是关于x的不等式组
)都是关于x的不等式组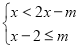 的关联方程,直接写出m的取值范围.
的关联方程,直接写出m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了进一步改进本校七年级数学教学,提高学生学习数学的兴趣,校教务处在七年级所有班级中,每班随机抽取了6名学生,并对他们的数学学习情况进行了问卷调查.我们从所调查的题目中,特别把学生对数学学习喜欢程度的回答(喜欢程度分为:“A﹣非常喜欢”、“B﹣比较喜欢”、“C﹣不太喜欢”、“D﹣很不喜欢”,针对这个题目,问卷时要求每位被调查的学生必须从中选一项且只能选一项)结果进行了统计,现将统计结果绘制成如下两幅不完整的统计图.

请你根据以上提供的信息,解答下列问题:(1)补全上面的条形统计图和扇形统计图;
(2)所抽取学生对数学学习喜欢程度的众数是 ;
(3)若该校七年级共有960名学生,请你估算该年级学生中对数学学习“不太喜欢”的有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.

求证:(1)△AFD≌△CEB.(2)四边形ABCD是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:我们把对非负实数
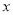 “四舍五入”到个位的值记为
“四舍五入”到个位的值记为 ,
,即当
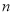 为非负整数时,若
为非负整数时,若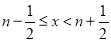 ,则
,则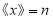 .
.例如:
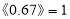 ,
,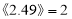 ,….
,….请解决下列问题:
(1)
 ______;
______;(2)若
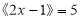 ,则实数
,则实数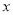 的取值范围是_________;
的取值范围是_________;(3)①
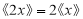 ;
;②当
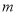 为非负整数时,
为非负整数时,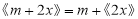 ;
;③满足
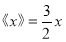 的非负实数
的非负实数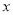 只有两个.其中结论正确的是_____(填序号)
只有两个.其中结论正确的是_____(填序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠1=∠2,要得到△ABD≌△ACE,从下列条件中补选一个,则错误的是( )

A.AB=AC B.DB=EC C.∠ADB=∠AEC D.∠B=∠C
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)已知
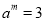 ,
,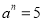 ,则
,则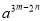 的值为_____________;
的值为_____________;(2)已知
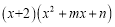 中,不含
中,不含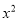 项和
项和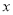 项,则
项,则 =______.
=______.
相关试题

