【题目】已知:如图,E、F是四边形ABCD的对角线AC上的两点,AF=CE,DF=BE,DF∥BE.

求证:(1)△AFD≌△CEB.(2)四边形ABCD是平行四边形.
参考答案:
【答案】证明见解析
【解析】证明:(1)∵DF∥BE,
∴∠DFE=∠BEF.
又∵AF=CE,DF=BE,
∴△AFD≌△CEB(SAS).
(2)由(1)知△AFD≌△CEB,
∴∠DAC=∠BCA,AD=BC,
∴AD∥BC.
∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形).
(1)利用两边和它们的夹角对应相等的两三角形全等(SAS),这一判定定理容易证明△AFD≌△CEB.
(2)由△AFD≌△CEB,容易证明AD=BC且AD∥BC,可根据一组对边平行且相等的四边形是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:等腰三角形OAB在直角坐标系中的位置如下图,点A的坐标为(
 ,3),点B的坐标为(﹣6,0).
,3),点B的坐标为(﹣6,0). 
(1)若△OAB关于y轴的轴对称图形是△OA'B',请直接写出A、B的对称点A'、B'的坐标;
(2)若将△OAB沿x轴向右平移a个单位,此时点A恰好落在反比例函数 的图象上,求a的值;
的图象上,求a的值;
(3)若△OAB绕点O按逆时针方向旋转30°,此时点B恰好落在反比例函数 的图象上,求k的值.
的图象上,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】罗山西亚丽宝超市第一次用5000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的
 倍多15件,甲、乙两种商品的进价和售价如下表:
倍多15件,甲、乙两种商品的进价和售价如下表: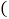 注:获利
注:获利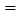 售价
售价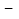 进价
进价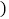
甲
乙
进价
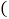 元
元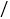 件
件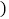
20
30
售价
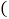 元
元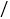 件
件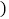
29
40
 罗山西亚丽宝超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
罗山西亚丽宝超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润? 该购物中心第二次以第一次的进价又购进甲、乙两种商品
该购物中心第二次以第一次的进价又购进甲、乙两种商品 其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多160元,求第二次乙种商品是按原价打几折销售?
其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多160元,求第二次乙种商品是按原价打几折销售? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.

(1)求二次函数解析式及顶点坐标;
(2)点P为线段BD上一点,若S△BCP= ,求点P的坐标;
,求点P的坐标;
(3)点M为抛物线上一点,作MN⊥CD,交直线CD于点N,若∠CMN=∠BDE,请直接写出所有符合条件的点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板按如图放置,则下列结论中,正确的有( )①∠1=∠3;②如果∠2=30°则有AC∥DE;③如果∠2=30°,则有BC∥AD;④如果∠2=30°,必有∠4=∠C

A.①②③B.①②④C.③④D.①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个全等的△ABC和△DEF重叠在一起,固定△ABC,将△DEF进行如下变换:
(1)如图1,△DEF沿直线CB向右平移(即点F在线段CB上移动),连接AF、AD、BD,请直接写出S△ABC与S四边形AFBD的关系;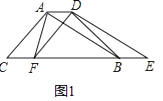
(2)如图2,当点F平移到线段BC的中点时,四边形AFBD是什么特殊四边形?请给出证明;
(3)当点F平移到线段BC的中点时,若四边形AFBD为正方形,猜想△ABC应满足什么条件?请直接写出结论:在此条件下,将△DEF沿DF折叠,点E落在FA的延长线上的点G处,连接CG,请在图3位置画出图形,并求出sin∠CGF的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】不等式组
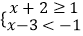 中的两个不等式的解集在同一个数轴上表示正确的是( )
中的两个不等式的解集在同一个数轴上表示正确的是( )
A.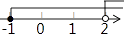
B.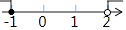
C.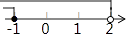
D.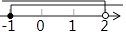
相关试题

