【题目】推理探索:(1)数轴上点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 分别表示数0、 2 、3、5、 4 ,解答下列问题.
分别表示数0、 2 、3、5、 4 ,解答下列问题.
①画出数轴表示出点![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ;
;
![]()
②![]() 、
、![]() 两点之间的距离是 ;
两点之间的距离是 ;
③![]() 、
、![]() 两点之间的距离是 ;
两点之间的距离是 ;
④![]() 、
、 ![]() 两点之间的距离是 ;
两点之间的距离是 ;
(2)请思考,若点![]() 表示数
表示数![]() 且
且![]() ,点
,点 ![]() 表示数
表示数![]() ,且
,且 ![]() ,则用含
,则用含 ![]() ,
,![]() 的代数式表示
的代数式表示 ![]() 、
、![]() 两点 间的距离是 ;
两点 间的距离是 ;
(3)请归纳,若点![]() 表示数
表示数![]() ,点
,点 ![]() 表示数
表示数![]() ,则
,则 ![]() 、
、![]() 两点间的距离用含
两点间的距离用含![]() 、
、![]() 的代数式表示是 .
的代数式表示是 .
参考答案:
【答案】(1)①见解析,②2,③2,④5;(2)![]() ;(3)
;(3)![]()
【解析】
(1)①画出数轴表示出点O,A、B、C、D即可;
②用O点表示的数减去A点表示的数即可得到结论.
③用C点表示的数减去B点表示的数即可得到结论.
④用B点表示的数减去A点表示的数即可得到结论.
(2)用B点表示的数减去A点表示的数即可得到结论.
(3)因为不知道A点表示的数与B点表示的数哪个数在右边,故其距离为|a-b|.
(1)①如图所示;
![]()
②O、A两点之间的距离是0-(-2)=2;
③C、B两点之间的距离是5-3=2;
④A、B两点之间的距离是3-(-2)=5;
(2)用含m,n的代数式表示A、B两点间的距离是n-m;
(3)A、B两点间的距离用含a、b的代数式表示是|a-b|;
故答案为: 2;2;5;n-m;|a-b|.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知线段
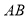 ,点
,点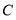 、点
、点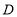 在直线
在直线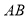 上,并且
上,并且 ,AC∶CB=1∶2,BD∶AB=2∶3,则AB=__________.
,AC∶CB=1∶2,BD∶AB=2∶3,则AB=__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点O为坐标原点,点B的坐标为(4,3),点A,C在坐标轴上,点P在BC边上,直线ι1:y=2x+3,直线ι2:y=2x-3
(1)求直线l1与x轴的交点坐标T,直线ι2与AB的交点坐标Q和与x轴的交点坐标G;
(2)判定四边形ATGQ的形状并求它的面积;
(3)已知点M在第一象限,且是直线l2上的点,若ΔAPM是等腰直角三角形,求点M坐标
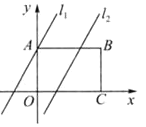
-
科目: 来源: 题型:
查看答案和解析>>【题目】有2部不同的电影A、B,甲、乙、丙3人分别从中任意选择1部观看.
(1)求甲选择A部电影的概率;
(2)求甲、乙、丙3人选择同一部电影的概率(请用画树状图的方法给出分析过程,并求出结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知C为线段AB的中点,E为线段AB上的点,点D为线段AE的中点.

(1)若线段AB=a,CE=b,|a﹣17|+(b﹣5.5)2=0,求线段AB、CE的长;
(2)如图1,在(1)的条件下,求线段DE的长;
(3)如图2,若AB=20,AD=2BE,求线段CE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AC,∠A=36°,AC的垂直平分线MN交AB于D,AC于M,以下结论:
①△BCD是等腰三角形;②射线CD是∠ACB的角平分线;③△BCD的周长C△BCD=AB+BC;④△ADM≌△BCD。
正确的有( )

A. ①② B. ①③ C. ①②③ D. ③④
相关试题

