【题目】在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
参考答案:
【答案】(1)每台电脑0.5万元,每台电子白板1.5万元(2)见解析
【解析】解:(1)设每台电脑x万元,每台电子白板y万元,根据题意得:
![]() , 解得:
, 解得:![]() 。
。
答:每台电脑0.5万元,每台电子白板1.5万元。
(2)设需购进电脑a台,则购进电子白板(30-a)台,
则![]() ,解得:
,解得:![]() ,即a=15,16,17。
,即a=15,16,17。
故共有三种方案:
方案一:购进电脑15台,电子白板15台.总费用为![]() 万元;
万元;
方案二:购进电脑16台,电子白板14台.总费用为![]() 万元;
万元;
方案三:购进电脑17台,电子白板13台.总费用为![]() 万元。
万元。
∴方案三费用最低。
(1)设电脑、电子白板的价格分别为x,y元,根据等量关系:“1台电脑+2台电子白板=3.5万元”,“2台电脑+1台电子白板=2.5万元”,列方程组求解即可。
(2)设计方案题一般是根据题意列出不等式组,求不等式组的整数解。设购进电脑x台,电子白板有(30-x)台,然后根据题目中的不等关系“总费用不超过30万元,但不低于28万元”列不等式组解答。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个正方体的展开图,标注了字母a的面是正方体的正面,如果正方体相对两个面上的整式的值相等,求整式(x+y)a的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD//BC,AC=8,BD=6.
(1)求证:四边形ABCD是平行四边形;
(2)若AC⊥BD,求□ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,F为BC边上一点,连接AF交DE于点G,下列说法不正确的是( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,连接AA′,若∠1=20°,则∠B的度数是( )
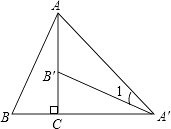
A.70°
B.65°
C.60°
D.55° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1=∠2,∠3=∠4,则下面结论中错误的是( )

A. △ADC≌△BCD B. △ABD≌△BAC C. △AOB≌△COD D. △AOD≌△BOC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,以AB为直径的⊙O与AC相交于点M,弦MN∥BC,与AB相交于点E,且ME=1,AM=2,AE=
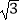 ,则弧BN的长为 .
,则弧BN的长为 . 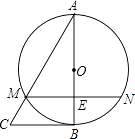
相关试题

