【题目】已知线段![]() ,点
,点![]() 、点
、点![]() 在直线
在直线![]() 上,并且
上,并且![]() ,AC∶CB=1∶2,BD∶AB=2∶3,则AB=__________.
,AC∶CB=1∶2,BD∶AB=2∶3,则AB=__________.
参考答案:
【答案】6或3
【解析】
要分三种情况进行讨论:①当C在线段AB上时,点D在线段AB的延长线上;②当点C在线段AB的反向延长线时,点D在AB上时;③当点C在线段AB的反向延长线,点D在线段AB的延长线时.
分三种情况进行讨论:
①当C在线段AB上时,点D在线段AB的延长线上,![]()
∵AC:CB=1:2,
∴BC=![]() AB,
AB,
∵BD:AB=2:3,
∴BD=![]() AB,
AB,
∴CD=BC+BD=![]() AB=8,
AB=8,
∴AB=6;
②当点C在线段AB的反向延长线时,![]()
∵BD:AB=2:3,
∴AB=3AD,
∵AC:CB=1:2,
∴AC=AB,
∴CD=AC+AD=4AD=8,
∴AD=2,
∴AB=6;
③当点C在线段AB的反向延长线,点D在线段AB的延长线时,![]()
∵AC:CB=1:2,BD:AB=2:3,
∴AB=![]() AB=3,
AB=3,
故AB=6或3.
故答案为:6或3
-
科目: 来源: 题型:
查看答案和解析>>【题目】课上老师提出一个问题:“如图,已知
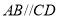 ,
,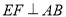 于点
于点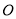 ,
,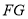 交
交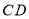 于点
于点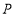 ,当
,当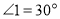 时,求
时,求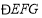 的度数.”
的度数.”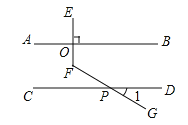
甲、乙、丙三位同学用不同的方法添加辅助线解决问题如图1,图2,图3所示.
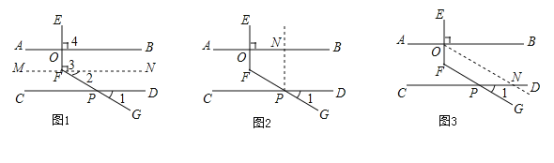
(1)补全甲同学的分析思路.
辅助线:过点
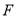 作
作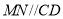 .
.分析思路:
①欲求∠EFG的度数,由图可知只需转化为求________和___________的度数之和;
②由辅助线作图可知
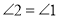 ;
;③由
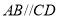 ,
,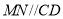 推出_________________,由此可推出
推出_________________,由此可推出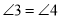 ;
;④由已知
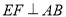 ,可得
,可得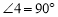 ,所以可得
,所以可得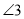 的度数,从而可求
的度数,从而可求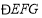 的度数.
的度数.(2)请你根据乙同学所画的辅助线,补全求解过程.
解:过
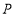 作___________________,交
作___________________,交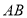 于点
于点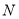 .
. ___________________________
___________________________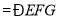 (两直线平行,同位角相等).
(两直线平行,同位角相等).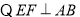 ,
,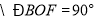 ,
,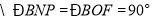 (_______________________).
(_______________________).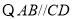 .
.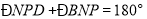 (____________________________),
(____________________________),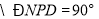 ,
,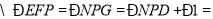 _______________________.
_______________________.(3)请你根据丙同学所画的辅助线,求
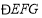 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形
 中,
中, 为平面直角坐标系的原点,点
为平面直角坐标系的原点,点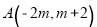 在
在 轴上,点
轴上,点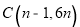 在
在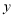 轴上,点
轴上,点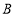 在第一象限内,点
在第一象限内,点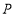 从原点出发,以每秒
从原点出发,以每秒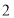 个单位长度的速度沿着
个单位长度的速度沿着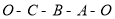 的路线移动(即沿着长方形的边移动一周).
的路线移动(即沿着长方形的边移动一周).(1)分别求出
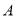 ,
,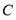 两点的坐标;
两点的坐标;(2)当点
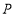 移动了
移动了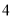 秒时,求出点
秒时,求出点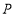 的坐标;
的坐标;(3)在移动过程中,当三角形
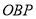 的面积是
的面积是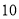 时,求满足条件的点
时,求满足条件的点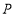 的坐标及相应的点
的坐标及相应的点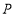 移动的时间.
移动的时间.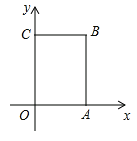
-
科目: 来源: 题型:
查看答案和解析>>【题目】在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几种购买方案,哪种方案费用最低.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,点O为坐标原点,点B的坐标为(4,3),点A,C在坐标轴上,点P在BC边上,直线ι1:y=2x+3,直线ι2:y=2x-3
(1)求直线l1与x轴的交点坐标T,直线ι2与AB的交点坐标Q和与x轴的交点坐标G;
(2)判定四边形ATGQ的形状并求它的面积;
(3)已知点M在第一象限,且是直线l2上的点,若ΔAPM是等腰直角三角形,求点M坐标
-
科目: 来源: 题型:
查看答案和解析>>【题目】推理探索:(1)数轴上点
 、
、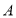 、
、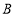 、
、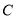 、
、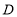 分别表示数0、 2 、3、5、 4 ,解答下列问题.
分别表示数0、 2 、3、5、 4 ,解答下列问题.①画出数轴表示出点
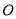 、
、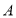 、
、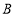 、
、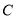 、
、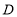 ;
;
②
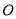 、
、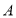 两点之间的距离是 ;
两点之间的距离是 ;③
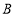 、
、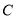 两点之间的距离是 ;
两点之间的距离是 ;④
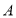 、
、 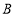 两点之间的距离是 ;
两点之间的距离是 ;(2)请思考,若点
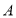 表示数
表示数 且
且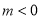 ,点
,点 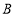 表示数
表示数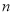 ,且
,且 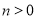 ,则用含
,则用含  ,
,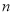 的代数式表示
的代数式表示  、
、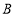 两点 间的距离是 ;
两点 间的距离是 ;(3)请归纳,若点
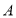 表示数
表示数 ,点
,点 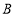 表示数
表示数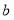 ,则
,则 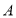 、
、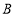 两点间的距离用含
两点间的距离用含 、
、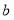 的代数式表示是 .
的代数式表示是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】有2部不同的电影A、B,甲、乙、丙3人分别从中任意选择1部观看.
(1)求甲选择A部电影的概率;
(2)求甲、乙、丙3人选择同一部电影的概率(请用画树状图的方法给出分析过程,并求出结果)
相关试题

