【题目】一天,小明和小红玩纸片拼图游戏.发现利用图①中的三种材料各若干可以拼出一些图形来解释某些等式,比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2.
(1)图③可以解释为等式: .
(2)图④中阴影部分的面积为 .观察图④请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 .
(3)如图⑤,小明利用7个长为b,宽为a的长方形拼成如图所示的大长方形;若AB=4,若长方形AGMB的面积与长方形EDHN的面积的差为S,试计算S的值(用含a,b的代数式表示)

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]() .
.
【解析】
(1)先求出大长方形的长、宽,再根据大长方形的面积等于四个正方形的面积与五个长方形的面积之和即可得;
(2)由图④可知,阴影部分为一个正方形,边长为![]() ,根据正方形的面积公式即可得;根据大正方形的面积等于小正方形的面积与四个长方形的面积之和即可得;
,根据正方形的面积公式即可得;根据大正方形的面积等于小正方形的面积与四个长方形的面积之和即可得;
(3)先根据长方形的面积公式求出长方形AGMB的面积、最大长方形的面积,再求出长方形EDHN的面积,两者作差即可得.
(1)由图可知,图③中大长方形的长为![]() ,宽为
,宽为![]()
则![]()
故答案为:![]() ;
;
(2)由图④可知,图④是由四个长方形和中间一个小正方形组成一个大正方形
大正方形的边长为![]() ,小正方形的边长为
,小正方形的边长为![]()
则阴影部分的面积为![]()
由大正方形的面积等于小正方形的面积与四个长方形的面积之和得:![]() ,即
,即![]()
故答案为:![]() ,
,![]() ;
;
(3)由图⑤可知,长方形AGMB的面积为![]()
最大长方形的面积为![]()
长方形EDHN的面积为![]()
则![]()
即![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在美化校园的活动中,某综合实践小组的同学借如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形的花圃ABCD(篱笆只围AB、BC两边)设AB=xm.
(1)若想围得花圃面积为192cm2,求x的值;
(2)若在点P处有一棵小树与墙CD、AD的距离分别为15m和6m,要将这棵树围在花圃内(含边界,不考虑树干的粗细),求花圃面积S的最大值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形 ABCD 中,∠BAD=α,∠BCD=180°-α,BD 平分∠ABC.
(1)如图,若α=90°,根据教材中一个重要性质直接可得 DA=CD,这个性质是 ;

(2)问题解决:如图,求证:AD=CD;

(3)问题拓展:如图,在等腰△ABC 中,∠BAC=100°,BD 平分∠ABC,求证:BD+AD=BC.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中有四边形ABCD.
(1)写出四边形ABCD的顶点坐标;
(2)求线段AB的长;
(3)求四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一批货物要运往某地,货主准备租用汽车运输公司的甲、乙两种货车,已知过去两次租用这两种货车的运货情况如下表:
第一次
第二次
甲种货车的辆数
2辆
5辆
乙种货车的辆数
3辆
6辆
累计运货重量
14吨
32吨
(1)分别求甲乙两种货车每辆载重多少吨?
(2)现租用该公司3辆甲种货车和5辆乙种货车刚好一次运完这批货物,如果按每吨付运费120元计算,货主应付运费多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,BC=2
 .点P从点A出发沿沿射线AB以1
.点P从点A出发沿沿射线AB以1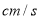 的速度运动,过点P作PE∥BC交射线AC于点E,同时点Q从点C出发沿BC的延长线以1
的速度运动,过点P作PE∥BC交射线AC于点E,同时点Q从点C出发沿BC的延长线以1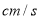 的速度运动,连结BE、EQ.设点P的运动时间为t(
的速度运动,连结BE、EQ.设点P的运动时间为t( ).
). 
(1)求证:△APE是等边三角形;
(2)直接写出CE的长(用含
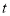 的代数式表示);
的代数式表示);(3)当点P在边AB上,且不与点A、B重合时,求证:△BPE≌△ECQ.
(4)在不添加字母和连结其它线段的条件下,当图中等腰三角形的个数大于3时,直接写出t的值和对应的等腰三角形的个数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,以O(0,0)、A(1,-1)、B(2,0)为顶点,构造平行四边形,下列各点中不能作为平行四边形第四个顶点坐标的是( )

A. (3,-1) B. (-1,-1) C. (1,1) D. (-2,-1)
相关试题

