【题目】如图,△ABC是等边三角形,BC=2![]() .点P从点A出发沿沿射线AB以1
.点P从点A出发沿沿射线AB以1![]() 的速度运动,过点P作PE∥BC交射线AC于点E,同时点Q从点C出发沿BC的延长线以1
的速度运动,过点P作PE∥BC交射线AC于点E,同时点Q从点C出发沿BC的延长线以1![]() 的速度运动,连结BE、EQ.设点P的运动时间为t(
的速度运动,连结BE、EQ.设点P的运动时间为t(![]() ).
).

(1)求证:△APE是等边三角形;
(2)直接写出CE的长(用含![]() 的代数式表示);
的代数式表示);
(3)当点P在边AB上,且不与点A、B重合时,求证:△BPE≌△ECQ.
(4)在不添加字母和连结其它线段的条件下,当图中等腰三角形的个数大于3时,直接写出t的值和对应的等腰三角形的个数.
参考答案:
【答案】(1)见解析;(2)2-t或t-2;(3)见解析;(4)当t=1时,图中有5个等腰三角形;当t=4时,图中有4个等腰三角形
【解析】
(1)根据等边三角形的性质可得∠A=∠ABC=∠ACB =60°,根据平行线的性质可得∠APE=∠ABC=60°,∠AEP=∠ACB=60°,再利用等边三角形的判定即可得证;
(2)由(1)可得AE=AP=t,分E没过C点与过C点两种情况进行解答即可;
(3)△ABC与△APE都是是等边三角形,利用等边三角形的性质易证BP=EC,∠BPE=∠ECQ=120°,再通过“边角边”证明△BPE≌△ECQ即可;
(4)当P在AB的中点,即t=1时,图中有5个等腰三角形;当P点在AP=2AB,即t=4时,图中有4个等腰三角形.
(1)∵△ABC是等边三角形,
∴∠A=∠ABC=∠ACB =60°,
∵![]() ,
,
∴∠APE=∠ABC=60°,∠AEP=∠ACB=60°.
∴△APE是等边三角形;
(2)∵△APE是等边三角形,
∴AE=AP=t,
当E点没过C点时,AE=2﹣t;
当E点过了C点时,AE=t﹣2;
(3)∵△ABC是等边三角形,
∴AB=AC,∠ACB=60°.
∵△APE是等边三角形,
∴AP=PE=AE,∠APE=60°.
∴AB-AP=AC-AE,∠BPE=∠ECQ=120°,
∴BP=EC,
∵AP=CQ=t,
∴PE=CQ,
∴△BPE≌ECQ(SAS);
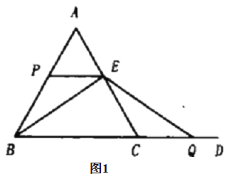
(4)如图1,当t=1时,图中有5个等腰三角形:△ABC,△APE,△PBE,△CQE,△EBQ;
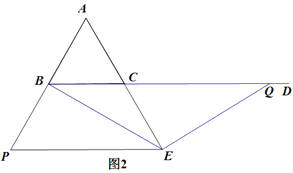
如图2,当t=4时,图中有4个等腰三角形:△ABC,△APE,△CBE,△EQB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中有四边形ABCD.
(1)写出四边形ABCD的顶点坐标;
(2)求线段AB的长;
(3)求四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一天,小明和小红玩纸片拼图游戏.发现利用图①中的三种材料各若干可以拼出一些图形来解释某些等式,比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2.
(1)图③可以解释为等式: .
(2)图④中阴影部分的面积为 .观察图④请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 .
(3)如图⑤,小明利用7个长为b,宽为a的长方形拼成如图所示的大长方形;若AB=4,若长方形AGMB的面积与长方形EDHN的面积的差为S,试计算S的值(用含a,b的代数式表示)

-
科目: 来源: 题型:
查看答案和解析>>【题目】一批货物要运往某地,货主准备租用汽车运输公司的甲、乙两种货车,已知过去两次租用这两种货车的运货情况如下表:
第一次
第二次
甲种货车的辆数
2辆
5辆
乙种货车的辆数
3辆
6辆
累计运货重量
14吨
32吨
(1)分别求甲乙两种货车每辆载重多少吨?
(2)现租用该公司3辆甲种货车和5辆乙种货车刚好一次运完这批货物,如果按每吨付运费120元计算,货主应付运费多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,以O(0,0)、A(1,-1)、B(2,0)为顶点,构造平行四边形,下列各点中不能作为平行四边形第四个顶点坐标的是( )

A. (3,-1) B. (-1,-1) C. (1,1) D. (-2,-1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,BC=a.作BC边的三等分点C1,使得CC1:BC1=1:2,过点C1作AC的平行线交AB于点A1,过点A1作BC的平行线交AC于点D1,作BC1边的三等分点C2,使得C1C2:BC2=1:2,过点C2作AC的平行线交AB于点A2,过点A2作BC的平行线交A1C1于点D2;如此进行下去,则线段AnDn的长度为______________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知任意一个三角形的三个内角的和是180°,如图1,在ABC中,∠ABC的角平分线BO与∠ACB的角平分线CO的交点为O.
(1)若∠A=70°,求∠BOC的度数;
(2)若∠A=α,求∠BOC的度数;
(3)如图2,若BO、CO分别是∠ABC、∠ACB的三等分线,也就是∠OBC=
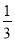 ∠ABC,∠OCB=
∠ABC,∠OCB=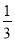 ∠ACB,∠A=α,求∠BOC的度数.
∠ACB,∠A=α,求∠BOC的度数.
相关试题

