【题目】已知:如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于G,且CD=AE.

(1)求证:CG=EG.
(2)求证:∠B=2∠ECB.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】
(1)连接DE,根据直角三角形的斜中定理得出DE=AE=BE,从而得出CD=DE,再利用斜中定理即可得出答案;
(2)根据DE=BE=CD,得出∠B=∠EDB,∠ECD=∠CED,即可得出答案.
证明:(1)
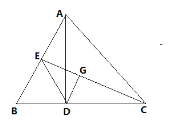
连接DE,∵AD⊥BC
∴△ABD为直角三角形
∵CE是AB边上的中线
∴E是直角三角形ABD斜边上的中线
则DE=AE=BE
又∵CD=AE
∴CD=DE
∵CD=DE,DG⊥CE
∴DE为等腰三角形底边上的中线,即CG=EG
(2)∵DE=BE=CD
∴∠B=∠EDB,∠ECD=∠CED
则∠B=∠EDB=2∠ECB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.
(1)求证:EF是⊙O切线;
(2)若AB=15,EF=10,求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解九年级学生的体能情况,学校组织了一次体能测试,并随机选取50名学生的成绩进行统计,得出相关统计表和统计图(其中部分数据不慎丢失,暂用字母m,n表示).
成绩等级
优秀
良好
合格
不合格
人数
m
30
n
5
请根据图表所提供的信息回答下列问题:
(1)统计表中的m= ,n= ;并补全频数分布直方图;
(2)若该校九年级有500名学生,请据此估计该校九年级学生体能良好以上的学生有多少人?
(3)根据以往经验,经过一段时间训练后,有60%的学生成绩可以上升一个等级,请估计经过训练后九年级学生体能达标率(成绩在良好及以上)

-
科目: 来源: 题型:
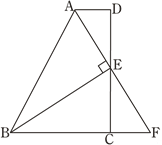
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F. 已知AD=2cm,BC=5cm.
(1)求证:FC=AD;
(2)求AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请阅读下列材料:已知方程x2+x﹣3=0,求一个一元二次方程,使它的根分别是已知方程根的2倍.
解:设所求方程的根为y,则y=2x.所以x=
 .
.把x=
 代入已知方程,得(
代入已知方程,得( )2+
)2+ ﹣3=0,化简,得y2+2y﹣12=0.
﹣3=0,化简,得y2+2y﹣12=0.故所求方程为y2+2y﹣12=0.
这种利用方程根的代换求新方程的方法,我们称为“换根法”.
问题:已知方程x2+x﹣1=0,求一个一元二次方程,使它的根分别是已知方程根的3倍.
-
科目: 来源: 题型:
查看答案和解析>>【题目】BD、CE分别是△ABC的边AC、AB上的高,P在BD的延长线上,且BP=AC,点Q在CE上,CQ=AB,
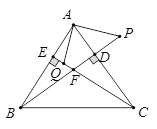
求证:(1)AP=AQ ;
(2)AP⊥AQ.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着人们生活质量的提高,净水器已经慢慢走入了普通百姓家庭,某电器公司销售每台进价分别为 2000 元,1700 元的A,B两种型号的净水器,下表是近两周的销售情况:
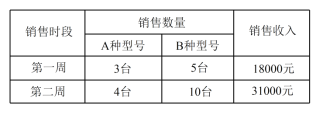
(1)求A,B两种型号的净水器的销售单价;
(2)若电器公司准备用不多于 54000 元的金额采购这两种型号的净水器共 30 台,求 A种型号的净水器最多能采购多少台?
(3)在(2)的条件下,公司销售完这 30 台净水器能否实现利润超过12800 元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
相关试题

