【题目】随着人们生活质量的提高,净水器已经慢慢走入了普通百姓家庭,某电器公司销售每台进价分别为 2000 元,1700 元的A,B两种型号的净水器,下表是近两周的销售情况:
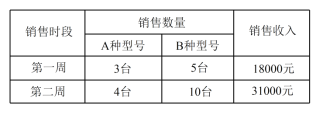
(1)求A,B两种型号的净水器的销售单价;
(2)若电器公司准备用不多于 54000 元的金额采购这两种型号的净水器共 30 台,求 A种型号的净水器最多能采购多少台?
(3)在(2)的条件下,公司销售完这 30 台净水器能否实现利润超过12800 元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
参考答案:
【答案】(1)A型2500元,B型2100元;(2)A型最多购买10台;(3)A型购买9台,B型购买21台;A型购买10台,B型购买20台
【解析】
(1)根据表格数据列出方程组即可得出答案;
(2)根据“若电器公司准备用不多于 54000 元的金额采购这两种型号的净水器共 30 台”,解不等式即可得出答案;
(3)在(2)的条件下,结合题意列出不等式,解不等式即可得出答案.
(1)解:设A、B型销售单价分别为x元和y元
![]() ,解得
,解得![]()
A型2500元,B型2100元;
(2)设A型采购量了m台
根据题意可得:2000m+1700(30-m)≤54000
解得m≤10,则A型最多购买10;
(3)500m+400(30-m)>12800,解得m>8
则当A型购买9台时,B型购买21台;A型购买10台时,B型购买20台.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,DG⊥CE于G,且CD=AE.

(1)求证:CG=EG.
(2)求证:∠B=2∠ECB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请阅读下列材料:已知方程x2+x﹣3=0,求一个一元二次方程,使它的根分别是已知方程根的2倍.
解:设所求方程的根为y,则y=2x.所以x=
 .
.把x=
 代入已知方程,得(
代入已知方程,得( )2+
)2+ ﹣3=0,化简,得y2+2y﹣12=0.
﹣3=0,化简,得y2+2y﹣12=0.故所求方程为y2+2y﹣12=0.
这种利用方程根的代换求新方程的方法,我们称为“换根法”.
问题:已知方程x2+x﹣1=0,求一个一元二次方程,使它的根分别是已知方程根的3倍.
-
科目: 来源: 题型:
查看答案和解析>>【题目】BD、CE分别是△ABC的边AC、AB上的高,P在BD的延长线上,且BP=AC,点Q在CE上,CQ=AB,
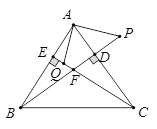
求证:(1)AP=AQ ;
(2)AP⊥AQ.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在Rt△ABC中,∠ACB=90°,AC=8,BC=16,D是AC上的一点,CD=3,点P从B点出发沿射线BC方向以每秒2个单位的速度向右运动.设点P的运动时间为t.连结AP.
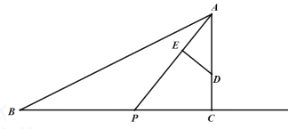
(1)当t=3秒时,求AP的长度(结果保留根号);
(2)当△ABP为等腰三角形时,求t的值;
(3)过点D做DE⊥AP于点E.在点P的运动过程中,当t为何值时,能使DE=CD?
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个一次函数y1=ax+b与y2=bx+a,它们在同一直角坐标系中的图象可能是( )
A.
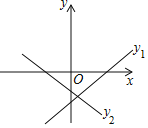 B.
B.
C.
 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程(x﹣3)(x﹣2)=|m|.
(1)求证:对于任意实数m,方程总有两个不相等的实数根;
(2)若方程的一个根是1,求m的值及方程的另一个根.
相关试题

