【题目】如图,已知抛物线y=ax2+bx﹣3的对称轴为直线x=1,交x轴于A、B两点,交y轴于C点,其中B点的坐标为(3,0). 
(1)直接写出A点的坐标;
(2)求二次函数y=ax2+bx﹣3的解析式.
参考答案:
【答案】
(1)解:∵抛物线y=ax2+bx﹣3的对称轴为直线x=1,交x轴于A、B两点,其中B点的坐标为(3,0),
∴A点横坐标为: ![]() =﹣1,
=﹣1,
∴A点的坐标为:(﹣1,0);
(2)解:将A(﹣1,0),B(3,0)代入y=ax2+bx﹣3得:
![]() ,
,
解得: ![]() .
.
故抛物线解析式为:y=x2﹣2x﹣3.
【解析】(1)根据抛物线的对称性直接写出点A的坐标;(2)把点A、B的坐标分别代入函数解析式列出关于a、b的方程组,通过解方程组来求它们的值.
【考点精析】解答此题的关键在于理解抛物线与坐标轴的交点的相关知识,掌握一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一天,某客运公司的甲、乙两辆客车分别从相距380千米的A、B两地同时出发相向而行,并以各自的速度匀速行驶,两车行驶2小时时甲车先到达服务区C地,此时两车相距20千米,甲车在服务区C地休息了20分钟,然后按原速度开往B地;乙车行驶2小时15分钟时也经过C地,未停留继续开往A地.(友情提醒:画出线段图帮助分析)
(1)乙车的速度是________千米/小时,B、C两地的距离是________千米, A、C两地的距离是________千米;
(2)求甲车的速度;
(3)这一天,乙车出发多长时间,两车相距200千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地区的电力资源丰富,并且得到了较好的开发.该地区一家供电公司为了鼓励居民用电,采用分段计费的方法来计算电费.月用电量x(度)与相应电费y(元)之间的函数图像如图所示.
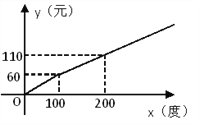
(1)月用电量为100度时,应交电费 元;
(2)当x≥100时,求y与x之间的函数关系式;
(3)月用电量为260度时,应交电费多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个自然数的立方,可以分裂成若干个连续奇数的和。例如:
 和
和 分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即
分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即 =3+5;
=3+5; =7+9+11;
=7+9+11; =13+15+17+19;…;若
=13+15+17+19;…;若 也按照此规律来进行“分裂”,则
也按照此规律来进行“分裂”,则 “分裂”出的奇数中,最大的奇数是______.
“分裂”出的奇数中,最大的奇数是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.
(1)求证:AD=AG;
(2)AD与AG的位置关系如何,请说明理由.

-
科目: 来源: 题型:
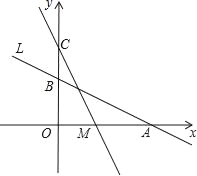
查看答案和解析>>【题目】如图,直线L:y=-
 x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.
x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A点以每秒1个单位的速度沿x轴向左移动.(1)求A、B两点的坐标;
(2)求△COM的面积S与M的移动时间t之间的函数关系式;
(3)当t为何值时△COM≌△AOB,并求此时M点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某市近郊有一块长为60米,宽为50米的矩形荒地,地方政府准备在此建一个综合性休闲广场,其中阴影部分为通道,通道的宽度均相等,中间的三个矩形(其中三个矩形的一边长均为a米)区域将铺设塑胶地面作为运动场地.
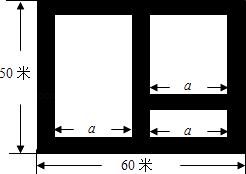
(1)设通道的宽度为x米,则a=(用含x的代数式表示);
(2)若塑胶运动场地总占地面积为2430平方米.请问通道的宽度为多少米?
相关试题

