【题目】某地区的电力资源丰富,并且得到了较好的开发.该地区一家供电公司为了鼓励居民用电,采用分段计费的方法来计算电费.月用电量x(度)与相应电费y(元)之间的函数图像如图所示.
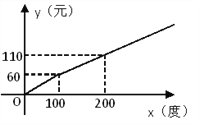
(1)月用电量为100度时,应交电费 元;
(2)当x≥100时,求y与x之间的函数关系式;
(3)月用电量为260度时,应交电费多少元?
参考答案:
【答案】(1)y=0.6x;(2)y=0.5x+10(x≥100);(3)140元.
【解析】试题分析:(1)根据函数图象,当x=100时,可直接从函数图象上读出y的值;
(2)设一次函数为:y=kx+b,将(100,60),(200,110)两点代入进行求解即可;
(3)将x=260代入(2)式所求的函数关系式进行求解可得出应交付的电费.
试题解析:(1)根据函数图象,知:当x=100时,y=60,故当月用电量为100时,应交付电费60元;
(2)设一次函数为y=kx+b,当x=100时,y=60;当x=200时,y=110
![]()
解得: ![]()
所求的函数关系式为: ![]()
(3)当x=260时,y=12×260+10=140
∴月用量为260度时,应交电费140元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】暑假期间,学校组织学生去某景点游玩,甲旅行社说:“如果带队的一名老师购买全票,则学生享受半价优惠”; 乙旅行社说:“所有人按全票价的六折优惠”.已知全票价为a元,学生有x人,带队老师有1人.
(1)试用含a和x的式子表示甲、乙旅行社的费用;
(2)若有50名学生参加本次活动,请你为他们选择一家更优惠的旅行社.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,BC为⊙O的直径,弦AD⊥BC于E,∠C=60°. 求证:△ABD为等边三角形.
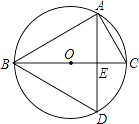
-
科目: 来源: 题型:
查看答案和解析>>【题目】一天,某客运公司的甲、乙两辆客车分别从相距380千米的A、B两地同时出发相向而行,并以各自的速度匀速行驶,两车行驶2小时时甲车先到达服务区C地,此时两车相距20千米,甲车在服务区C地休息了20分钟,然后按原速度开往B地;乙车行驶2小时15分钟时也经过C地,未停留继续开往A地.(友情提醒:画出线段图帮助分析)
(1)乙车的速度是________千米/小时,B、C两地的距离是________千米, A、C两地的距离是________千米;
(2)求甲车的速度;
(3)这一天,乙车出发多长时间,两车相距200千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个自然数的立方,可以分裂成若干个连续奇数的和。例如:
 和
和 分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即
分别可以按如图所示的方式“分裂”成2个、3个和4个连续奇数的和,即 =3+5;
=3+5; =7+9+11;
=7+9+11; =13+15+17+19;…;若
=13+15+17+19;…;若 也按照此规律来进行“分裂”,则
也按照此规律来进行“分裂”,则 “分裂”出的奇数中,最大的奇数是______.
“分裂”出的奇数中,最大的奇数是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx﹣3的对称轴为直线x=1,交x轴于A、B两点,交y轴于C点,其中B点的坐标为(3,0).

(1)直接写出A点的坐标;
(2)求二次函数y=ax2+bx﹣3的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD、AG.
(1)求证:AD=AG;
(2)AD与AG的位置关系如何,请说明理由.

相关试题

