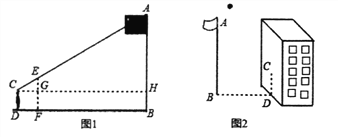
【题目】数学兴趣小组测量校园内旗杆的高度,有以下两种方案:
方案一:小明在地面上直立一根标杆![]() ,沿着直线
,沿着直线![]() 后退到点
后退到点![]() ,使眼睛
,使眼睛![]() 、标杆的顶点
、标杆的顶点![]() 、旗杆的顶点
、旗杆的顶点![]() 在同一直线上(如图1).测量:人与标杆的距离
在同一直线上(如图1).测量:人与标杆的距离![]() =1 m,人与旗杆的距离
=1 m,人与旗杆的距离![]() =16m,人的目高和标杆的高度差
=16m,人的目高和标杆的高度差![]() =0.9m,人的高度
=0.9m,人的高度![]() =1.6m.
=1.6m.
方案二:小聪在某一时刻测得1米长的竹竿竖直放置时影长1.5米,在同时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上影长为21米,留在墙上的影高为2米(如图2).
请你结合上述两个方案,选择其中的一个方案求旗杆的高度。我选择方案 .
参考答案:
【答案】见解析
【解析】方案一:由题意得出CD∥EF∥AB,证出△ECG∽△ACH,得出对应边成比例![]() ,求出AH,即可得出结果;
,求出AH,即可得出结果;
方案二:延长AC,BD相交于点E,则CD:DE=1:1.5,得DE=1.5CD=3米,由CD∥AB,得出△ABE∽△CDE,得出对应边成比例![]() ,即可得出结果.
,即可得出结果.
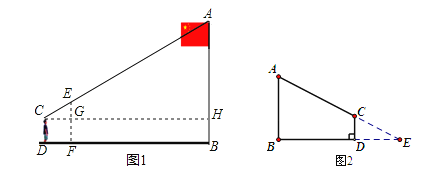
方案一:如图1所示:
由已知得:CD∥EF∥AB,∴△ECG∽△ACH,∴![]() ,即
,即![]() ,解得:AH=14.4米,∴AB=AH+BH=14.4+1.6=16(米);
,解得:AH=14.4米,∴AB=AH+BH=14.4+1.6=16(米);
答:旗杆的高度是16米;
方案二:如图所示,延长AC,BD相交于点E,则CD:DE=1:1.5,得DE=1.5CD=3米,由已知CD∥AB,∴△ABE∽△CDE,∴![]() ,即
,即![]() ,解得:AB=16.
,解得:AB=16.
答:旗杆的高度是16米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A=2a2+3ab﹣2a﹣1,B=﹣a2+
 ab+
ab+ .
.(1)a=﹣1,b=﹣2时,求4A﹣(3A﹣2B)的值;
(2)若(1)中式子的值与a的取值无关,求b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列各等式:
13=1=
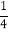 ×11×22
×11×2213+23=9=
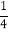 ×22×32
×22×3213+23+33=36=
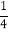 ×32×42
×32×42…
用你发现的规律解答下列问题:
(1)填空:13+23+33+…+(n﹣1)3+n3=
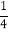 ×( )2×( )2(n为正整数);
×( )2×( )2(n为正整数);(2)计算:
①13+23+33+…+493+503;
②23+43+63+…+983+1003
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
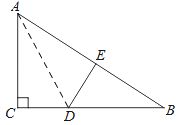
(1)求证:△BDE∽△BAC;
(2)已知AC=6,BC=8,求线段AD的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂一周计划每日生产某产品100吨,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的吨数记为正数,减少的吨数记为负数)
星期
一
二
三
四
五
六
日
增减/吨
﹣1
+3
﹣2
+4
+7
﹣5
﹣10
(1)生产量最多的一天比生产量最少的一天多生产多少吨?
(2)本周总生产量是多少吨?比原计划增加了还是减少了?增减数为多少吨?
(3)若本周总生产的产品全部由35辆货车一次性装载运输离开工厂,则平均每辆货车大约需装载多少吨?(结果精确到0.01吨)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)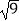 ﹣
﹣ 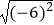 ﹣
﹣ 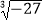
(2)(x+1)2=64
(3)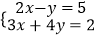
(4)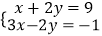
(5)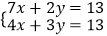
(6) .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个自然数的立方,可以分裂成若干个连续奇数的和,例如:23,33和43分别可以按如图所示的方式“分裂”,则63“分裂”出的奇数中,最大的奇数是_____.

相关试题

