搜索
【题目】已知A=2a2+3ab﹣2a﹣1，B=﹣a2+
ab+
．
（1）a=﹣1，b=﹣2时，求4A﹣（3A﹣2B）的值；
（2）若（1）中式子的值与a的取值无关，求b的值．
参考答案：
【答案】（1）4ab﹣2a+
；（2）b=
【解析】
（1）将a=﹣1，b=﹣2代入A=2a2+3ab﹣2a﹣1，B=﹣a2+ab+
，求出A、B的值，再计算4A﹣（3A﹣2B）的值即可；（2）把（1）结果变形，根据结果与a的值无关求出b的值即可.
（1）4A﹣（3A﹣2B）
=4A﹣3A+2B
=A+2B，
∵A=2a2+3ab﹣2a﹣1，B=﹣a2+ab+，
∴A+2B
=2a2+3ab﹣2a﹣1+2（﹣a2+ab+）
=2a2+3ab﹣2a﹣1﹣2a2+ab+
=4ab﹣2a+；
（2）因为4ab﹣2a+
=（4b﹣2）a+，
又因为4ab﹣2a+的值与a的取值无关，
所以4b﹣2=0，
所以b=．
-
科目： 来源： 题型：
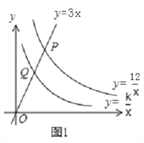
查看答案和解析>>【题目】如图1，已知直线y=3x分别与双曲线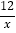y=
、y=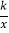
（x＞0）交于P、Q两点，且OP=2OQ．（1）求k的值．
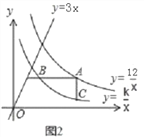
（2）如图2，若点A是双曲线y=
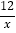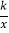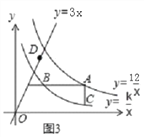
上的动点，AB∥x轴，AC∥y轴，分别交双曲线y=（x＞0）于点B、C，连接BC．请你探索在点A运动过程中，△ABC的面积是否变化？若不变，请求出△ABC的面积；若改变，请说明理由； （3）如图3，若点D是直线y=3x上的一点，请你进一步探索在点A运动过程中，以点A、B、C、D为顶点的四边形能否为平行四边形？若能，求出此时点A的坐标；若不能，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在数轴上，点A、B表示的数分别是有理数a，b．
（1）若点A在原点的左侧，点B在原点的右侧，且|a|=|b|，则a与b的关系是 ，用式子表示为 ．
（2）若a=﹣5，b=1
①分别写出a，b的相反数；
②求|a
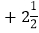|﹣|b
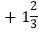|的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，
的面积为9，点
在的边上运动.作点关于原点
的对称点
，再以
为边作等边
.当点在的边上运动一周时，点
随之运动所形成的图形面积为（ ）
A. 3 B. 9 C. 27 D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】观察下列各等式：
13=1=
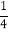×11×2213+23=9=
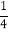×22×3213+23+33=36=
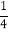×32×42…
用你发现的规律解答下列问题：
（1）填空：13+23+33+…+（n﹣1）3+n3=
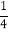×（ ）2×（ ）2（n为正整数）；（2）计算：
①13+23+33+…+493+503；
②23+43+63+…+983+1003
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠C=90°，△ACD沿AD折叠，使得点C落在斜边AB上的点E处．
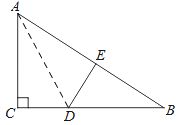
（1）求证：△BDE∽△BAC；
（2）已知AC=6，BC=8，求线段AD的长度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】数学兴趣小组测量校园内旗杆的高度，有以下两种方案:
方案一:小明在地面上直立一根标杆
,沿着直线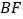
后退到点
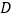，使眼睛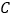
、标杆的顶点
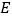、旗杆的顶点
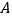在同一直线上(如图1).测量:人与标杆的距离
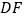=1 m，人与旗杆的距离
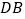=16m，人的目高和标杆的高度差
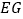=0.9m，人的高度
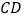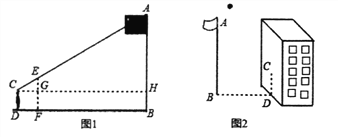
=1.6m.方案二:小聪在某一时刻测得1米长的竹竿竖直放置时影长1.5米，在同时刻测量旗杆的影长时，因旗杆靠近一楼房，影子不全落在地面上，有一部分落在墙上，他测得落在地面上影长为21米，留在墙上的影高为2米(如图2).
请你结合上述两个方案，选择其中的一个方案求旗杆的高度。我选择方案 .
相关试题
