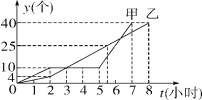
【题目】某车间的甲、乙两名工人分别同时生产同种零件,他们一天生产零件y(个)与生产时间t(小时)的关系如图所示.
(1)根据图象回答:
①甲、乙中,谁先完成一天的生产任务;在生产过程中,谁因机器故障停止生产多少小时;
②当t等于多少时,甲、乙所生产的零件个数相等;
(2)谁在哪一段时间内的生产速度最快?求该段时间内,他每小时生产零件的个数.
参考答案:
【答案】(1) ①甲,甲,3小时;②3和![]() ; (2) 甲在5~7时的生产速度最快,每小时生产零件15个.
; (2) 甲在5~7时的生产速度最快,每小时生产零件15个.
【解析】
(1)根据图象不难得出结论;
(2)从图上看出甲在5~7时直线斜率最大,即生产速度最快.
解:(1) ①甲、乙中,甲先完成一天的生产任务;在生产过程中,甲因机器故障停止生产3小时;
②由图象可知,甲、乙两条折线相交时,表示甲、乙所生产的零件个数相等.
当t=3时,甲乙第一次相交;
设甲乙第二次相交时生产时间为t2,得:
10+![]() =4+
=4+![]() (
(![]() -2),
-2),
解得:t2=![]() ,
,
∴当t等于3和![]() 时,甲、乙所生产的零件个数相等;
时,甲、乙所生产的零件个数相等;
(2)甲在5~7时的生产速度最快,
∵(40-10)÷(7-5)=15,
∴他在这段时间内每小时生产零件15个.
故答案为:(1) ①甲,甲,3小时;②3和![]() ; (2) 甲在5~7时的生产速度最快,每小时生产零件15个.
; (2) 甲在5~7时的生产速度最快,每小时生产零件15个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】衢州市新农村建设推动了农村住宅旧貌变新颜,如图为一农村民居侧面截图,屋坡AF、AG分别架在墙体的点B、点C处,且AB=AC,侧面四边形BDEC为矩形.若测得∠FAG=110°,则∠FBD=( )
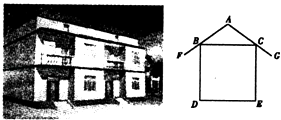
A.35°
B.40°
C.55°
D.70° -
科目: 来源: 题型:
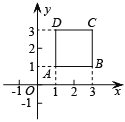
查看答案和解析>>【题目】如图所示,正方形ABCD的顶点坐标分别为A(1,1),B(3,1),C(3,3),D(1,3).
(1)在同一直角坐标系中,将正方形向左平移2个单位,画出相应的图形,并写出各点的坐标.
(2)将正方形向下平移2个单位,画出相应的图形,并写出各点的坐标.
(3)在(1)(2)中,你发现各点的横、纵坐标发生了哪些变化?
-
科目: 来源: 题型:
查看答案和解析>>【题目】圣诞老人上午8:00从家里出发,骑车去一家超市购物,然后从这家超市回到家中,圣诞老人离家的距离s(千米)和所经过的时间t(分钟)之间的关系如图所示,请根据图象回答问题:
(1)圣诞老人去超市途中的速度是多少?回家途中的速度是多少?
(2)圣诞老人在超市逗留了多长时间?
(3)圣诞老人在来去的途中,离家2千米处的时间是几时几分?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△ADE中,点E在BC边上,∠BAC=∠DAE,∠B=∠D, AB=AD.
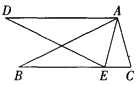
(1)试说明△ABC≌△ADE;
(2)如果∠AEC=75°,将△ADE绕点A旋转一个锐角后与△ABC重合,求这个旋转角的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连接OA,OB,OC.
(1)若△ADE的周长为6 cm,△OBC的周长为16 cm.
①求线段BC的长;
②求线段OA的长.
(2)若∠BAC=120°,求∠DAE的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得到一些有用的式子,或可以求出一些不规则图形的面积.

(1)如图1,是将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的方法计算这个图形的面积,你能发现什么结论,请写出来.
(2)如图2,是将两个边长分别为a和b的正方形拼在一起,B、C、G三点在同一直线上,连接BD和BF,若两正方形的边长满足a+b=10,ab=20,你能求出阴影部分的面积吗?
相关试题

