【题目】如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连接OA,OB,OC.
(1)若△ADE的周长为6 cm,△OBC的周长为16 cm.
①求线段BC的长;
②求线段OA的长.
(2)若∠BAC=120°,求∠DAE的度数.

参考答案:
【答案】(1) ①6cm; ②5cm;(2) 60°
【解析】
(1)①根据垂直平分线性质得AD=BD、EA=EC,由△ADE的周长为6 cm,即可解题,
②根据垂直平分线性质得OA=OB、OA=OC,由△OBC的周长为16 cm,即可解题,
(2)根据等边对等角,证明∠BAD=∠ABC,∠EAC=∠ACB,利用∠BAC=120°,三角形内角和即可解题.
(1)①因为l1是AB边的垂直平分线,所以AD=BD.
因为l2是AC边的垂直平分线,
所以EA=EC,
所以BC=BD+DE+EC=AD+DE+EA=6 cm.
②因为l1是AB边的垂直平分线,
所以OA=OB.
因为l2是AC边的垂直平分线,所以OA=OC.
因为OB+OC+BC=16 cm,
由(1)知,BC=6 cm,
所以OA=OB=OC=5 cm.
(2)因为∠BAC=120°,
所以∠ABC+∠ACB=60°.
因为AD=BD,EA=EC,
所以∠BAD=∠ABC,∠EAC=∠ACB,
所以∠DAE=∠BAC-∠BAD-∠EAC=∠BAC-∠ABC-∠ACB=60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】圣诞老人上午8:00从家里出发,骑车去一家超市购物,然后从这家超市回到家中,圣诞老人离家的距离s(千米)和所经过的时间t(分钟)之间的关系如图所示,请根据图象回答问题:
(1)圣诞老人去超市途中的速度是多少?回家途中的速度是多少?
(2)圣诞老人在超市逗留了多长时间?
(3)圣诞老人在来去的途中,离家2千米处的时间是几时几分?

-
科目: 来源: 题型:
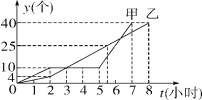
查看答案和解析>>【题目】某车间的甲、乙两名工人分别同时生产同种零件,他们一天生产零件y(个)与生产时间t(小时)的关系如图所示.
(1)根据图象回答:
①甲、乙中,谁先完成一天的生产任务;在生产过程中,谁因机器故障停止生产多少小时;
②当t等于多少时,甲、乙所生产的零件个数相等;
(2)谁在哪一段时间内的生产速度最快?求该段时间内,他每小时生产零件的个数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△ADE中,点E在BC边上,∠BAC=∠DAE,∠B=∠D, AB=AD.
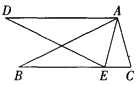
(1)试说明△ABC≌△ADE;
(2)如果∠AEC=75°,将△ADE绕点A旋转一个锐角后与△ABC重合,求这个旋转角的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得到一些有用的式子,或可以求出一些不规则图形的面积.

(1)如图1,是将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的方法计算这个图形的面积,你能发现什么结论,请写出来.
(2)如图2,是将两个边长分别为a和b的正方形拼在一起,B、C、G三点在同一直线上,连接BD和BF,若两正方形的边长满足a+b=10,ab=20,你能求出阴影部分的面积吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC.
① 求证:△ABE≌△CBD;
② 若∠CAE=30°,求∠BDC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】5月19日为中国旅游日,衢州推出“读万卷书,行万里路,游衢州景”的主题系列旅游惠民活动,市民王先生准备在优惠日当天上午从孔氏南宗家庙、烂柯山、龙游石窟中随机选择一个地点;下午从江郎山、三衢石林、开化根博园中随机选择一个地点游玩,则王先生恰好上午选中孔氏南宗家庙,下午选中江郎山这两个地的概率是( )
A.
B.
C.
D.
相关试题

